Enhanced Cycle and Tour Functionality
Plan an inspection tour to visit border posts shared by countries at least once and minimize the travel length.
| In[1]:= |  X |
| In[2]:= | X |
| In[3]:= | X |
| Out[3]//Short= |
| In[4]:= | X |
| Out[4]= | 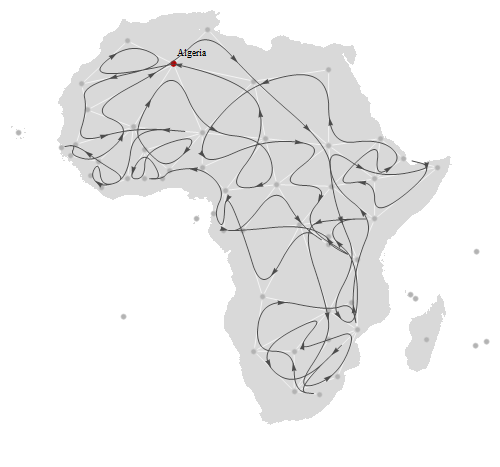 |
| « View all new features in Mathematica 9 | ◄ previous | next ► |
| In[1]:= |  X |
| In[2]:= | X |
| In[3]:= | X |
| Out[3]//Short= |
| In[4]:= | X |
| Out[4]= |  |