New and Enhanced Graph Layouts
Adding to an already rich set of graph layouts, Mathematica 9 brings new capabilities to visualize graphs with structures such as planar graphs, multipartite graphs, and trees.
| In[1]:= |  X |
| Out[1]= | 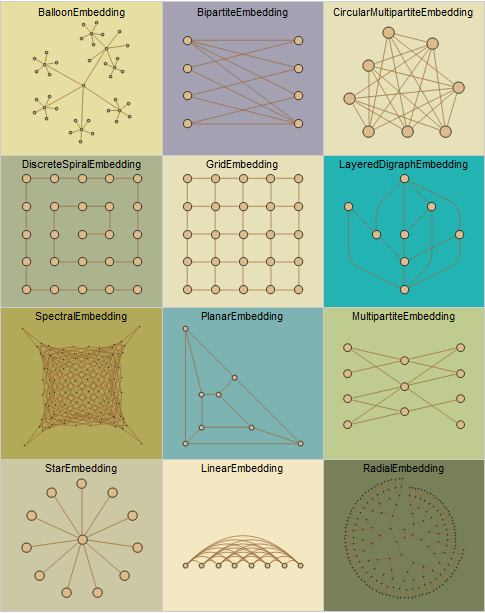 |
| « View all new features in Mathematica 9 | ◄ previous | next ► |
| In[1]:= |  X |
| Out[1]= |  |