Boundary Value Solutions
| In[4]:= |  X |
Find the solutions of a parametric equation that satisfy a Dirichlet boundary condition.
| In[1]:= | 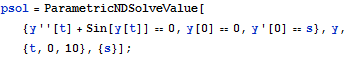 X |
| In[2]:= | X |
| Out[2]= | 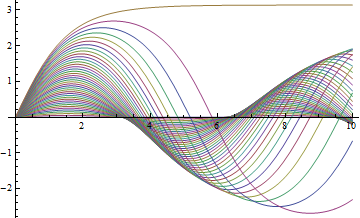 |
A parameter sweep determines the nontrivial solution values of 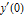 .
.
| In[3]:= |  X |
| Out[3]= |
| Out[4]= | 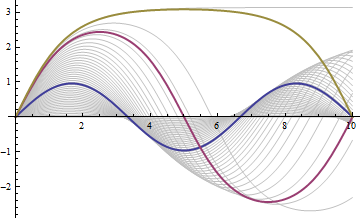 |
| « View all new features in Mathematica 9 | ◄ previous | next ► |
| In[4]:= |  X |
| In[1]:= | 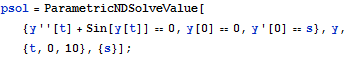 X |
| In[2]:= | X |
| Out[2]= |  |
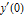 .
.| In[3]:= |  X |
| Out[3]= |
| Out[4]= |  |