Minimal Arc Length Solution 

In[4]:=

X Show[{Plot[ Evaluate@Table[y[a][t] /. psol, {a, .65, .8, .005}], {t, 0, 10}, PlotStyle -> Lighter[Gray, 0.5]], Plot[Evaluate[y[a][t] /. psol /. lmin[[2]]], {t, 0, 10}, PlotStyle -> Thick]}, ImageSize -> Medium]

Plot the arc length of the solution against a parameter value in a parametric equation.

In[1]:=

X psol = ParametricNDSolve[{y''[t] + y[t] == 3 a Sin[y[t]], y[0] == y'[0] == 1, \[Alpha]'[t] == Sqrt[1 + y[t]^2], \[Alpha][0] == 0}, {y, \[Alpha]}, {t, 0, 10}, {a}];

In[2]:=

X GraphicsRow[{Plot[ Evaluate@Table[y[a][t] /. psol, {a, 0, 1, .1}], {t, 0, 10}, ImageSize -> Small], Plot[Evaluate[\[Alpha][a][10] /. psol], {a, 0, 1}, MaxRecursion -> 0, PlotPoints -> 100, AxesLabel -> {a, \[Alpha]}, ImageSize -> Small]}]

Out[2]=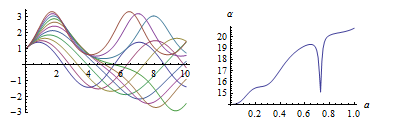

Find the solution corresponding to the locally minimal arc length near a=.725.

In[3]:=

X lmin = FindMinimum[\[Alpha][a][10] /. psol, {a, 0.72}, AccuracyGoal -> 7]

Out[3]=

Out[4]=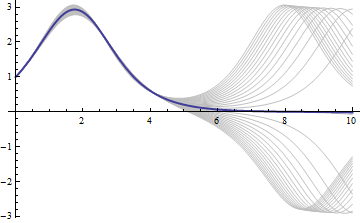