Parameter Fitting
Find the parameter 
that gives the best fit for given data to the Van der Pol equation.
that gives the best fit for given data to the Van der Pol equation.| In[1]:= |  X |
| In[2]:= |  X |
| Out[2]= |  |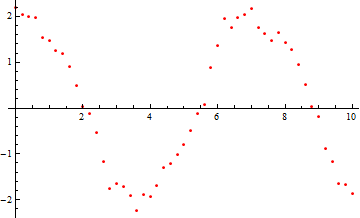
Create a ParametricFunction object and use it in FindFit.
| In[3]:= |  X |
| In[4]:= |  X |
| Out[4]= |  |
| In[5]:= |  X |
| Out[5]= | 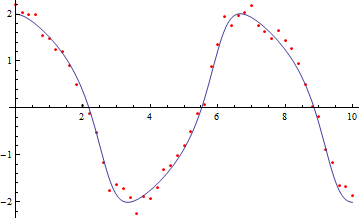 |