Parametric Dependence
Plot the dependence of 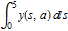 on a parameter a in the differential equation.
on a parameter a in the differential equation.
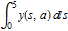 on a parameter a in the differential equation.
on a parameter a in the differential equation.| In[2]:= | 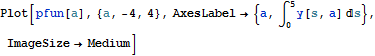 X |
| In[3]:= | 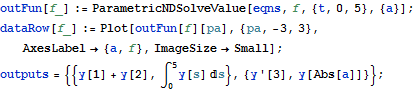 X |
| In[4]:= | X |
| In[1]:= |  X |
| Out[2]= | 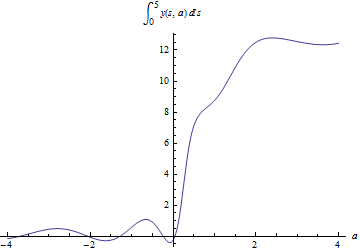 |
Find the dependence of several other expressions on the parameter a.
| Out[4]= | 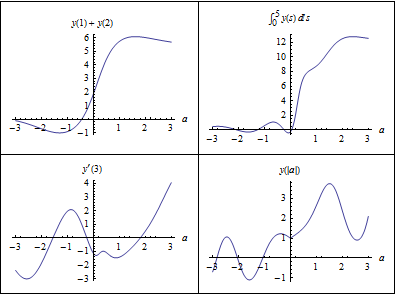 |