Parameterize Anywhere 

In[6]:=

X freqplot = {x''[t] == -Framed[\[Omega]] x[t], Plot[Evaluate@ Table[pfun[\[Omega], 1, 0, 10][t], {\[Omega], .5, 3, .5}], {t, 0, 4 \[Pi]}, Ticks -> None]}; initvalplot = {x[0] == Framed[x0], Plot[Evaluate@Table[pfun[1, x0, 0, 10][t], {x0, -1, 1, .1}], {t, 0, 4 \[Pi]}, Ticks -> None]}; initderplot = {x'[0] == Framed[x1], Plot[Evaluate@Table[pfun[1, 0, x1, 10][t], {x1, -1, 1, .1}], {t, 0, 4 \[Pi]}, Ticks -> None]}; wpplot = {WorkingPrecision -> Framed[wp], ListLogPlot[ Table[{wp, Abs[pfun[1, 1, 0, wp][4 \[Pi]] - 1]}, {wp, 16, 60}], AxesLabel -> {wp, "Error"}, Ticks -> None]};

Parameters can replace numeric quantities throughout the problem specification.

In[1]:=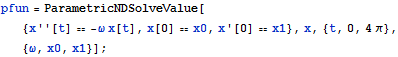

X pfun = ParametricNDSolveValue[{x''[t] == -\[Omega] x[t], x[0] == x0, x'[0] == x1}, x, {t, 0, 4 \[Pi]}, {\[Omega], x0, x1}];

Vary the frequency parameter.

In[2]:=

X Plot[Evaluate@ Table[pfun[\[Omega], 1, 0][t], {\[Omega], .5, 3, .5}], {t, 0, 4 \[Pi]}, ImageSize -> Medium]

Out[2]=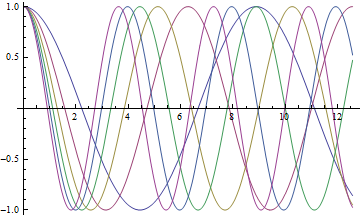

Vary the initial condition parameters.

In[3]:=

X GraphicsColumn[{Plot[ Evaluate@Table[pfun[1, x0, 0][t], {x0, -1, 1, .1}], {t, 0, 4 \[Pi]}, ImageSize -> Medium], Plot[Evaluate@Table[pfun[1, 0, x1][t], {x1, -1, 1, .1}], {t, 0, 4 \[Pi]}, ImageSize -> Medium]}]

Out[3]=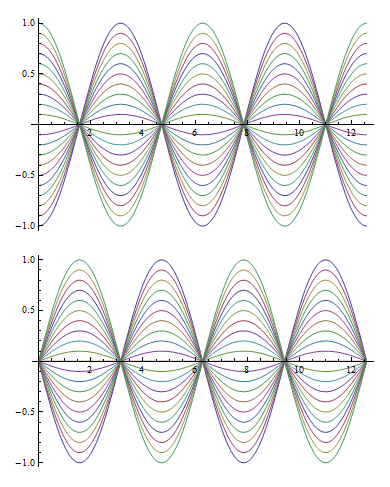

Vary the working precision parameter.

In[4]:=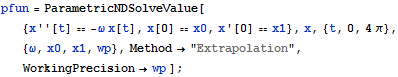

X pfun = ParametricNDSolveValue[{x''[t] == -\[Omega] x[t], x[0] == x0, x'[0] == x1}, x, {t, 0, 4 \[Pi]}, {\[Omega], x0, x1, wp}, Method -> "Extrapolation", WorkingPrecision -> wp ];

In[5]:=

X ListLogPlot[ Table[{wp, Abs[pfun[1, 1, 0, wp][4 \[Pi]] - 1]}, {wp, 16, 60}], AxesLabel -> {wp, "Error"}, ImageSize -> Medium]

Out[5]=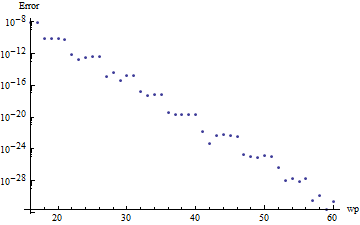