Sensitivity of a Parametric Wave Equation
| In[2]:= |  X |
| In[3]:= | 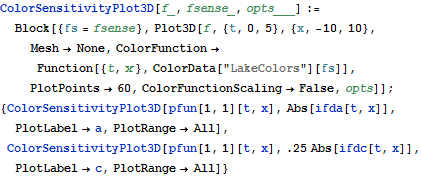 X |
Find and plot the parametric sensitivity of a parameterized wave equation.
| In[1]:= |  X |
Show the sensitivity to the initial wave height a and wave speed c.
| Out[2]= |  |
Another way to visualize the solution sensitivity is to vary the color of the solution surface.
| Out[3]= |  |