Standard Deviation Function for Processes
The standard deviation function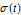 
for a process 
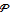is given by StandardDeviation[
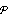[t]].
A discrete-time and discrete-state random process.
| In[1]:= |  X |
| Out[1]= |  |
| In[2]:= |  X |
| Out[2]= |  |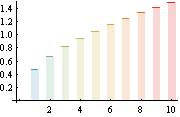
A discrete-time and continuous-state random process.
| In[3]:= |  X |
| Out[3]= |  |
| In[4]:= |  X |
| Out[4]= |  |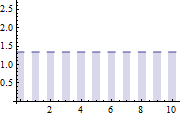
A continuous-time and discrete-state random process.
| In[5]:= |  X |
| Out[5]= |  |
| In[6]:= |  X |
| Out[6]= |  |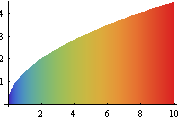
A continuous-time and continuous-state random process.
| In[7]:= |  X |
| Out[7]= |  |
| In[8]:= |  X |
| Out[8]= | 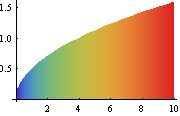 |