pts = {{0, 0}, {1, 1}, {2, -1}, {3, 1}, {4, -1}, {5, 1}, {3, 2}};
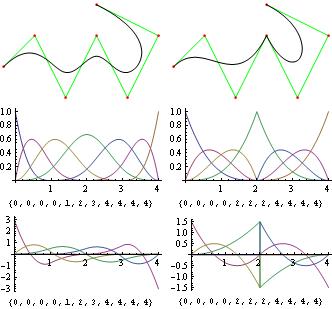
knots1 = {0, 0, 0, 0, 1, 2, 3, 4, 4, 4, 4};
knots2 = {0, 0, 0, 0, 2, 2, 2, 4, 4, 4, 4};
drawcurve[p_, k_] :=
Graphics[{Green, Line[p], Red, Point[p], Black,
BSplineCurve[p, SplineDegree -> 3, SplineKnots -> k]}]
drawbasis[k_] :=
Labeled[Plot[
Evaluate@Table[BSplineBasis[{3, k}, i, x], {i, 0, 6}], {x, 0, 4},
PlotRange -> All, AspectRatio -> 1/2], Style[k, Small]];
drawders[k_] :=
Quiet[Labeled[
Plot[Evaluate@
Table[D[BSplineBasis[{3, k}, i, x], x], {i, 0, 6}], {x, 0, 4},
PlotRange -> All, AspectRatio -> 1/2], Style[k, Small]]];
Grid[{{drawcurve[pts, knots1],
drawcurve[pts, knots2]}, {drawbasis[knots1],
drawbasis[knots2]}, {drawders[knots1], drawders[knots2]}}]