New in Wolfram Mathematica 7: Comprehensive Spline Support ◄ previous | next ►
Use Splines for Interpolation
Using spline methods in Interpolation, highly continuous results are achievable with relatively low degrees.
In[1]:=

Click for copyable input
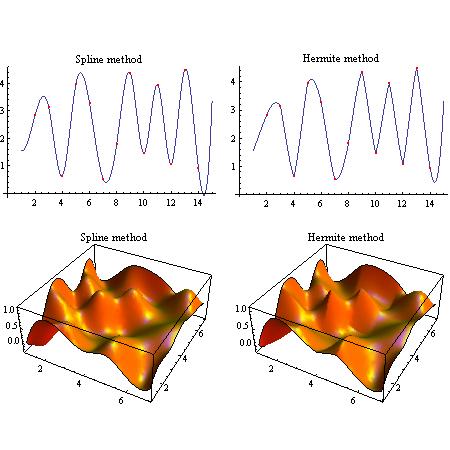
SeedRandom[4]; data = RandomReal[5, {15}];

f = Interpolation[data, Method -> "Spline"];

g = Interpolation[data, Method -> "Hermite"];

drawfun[f_, t_] := 

  Plot[f[x], {x, 1, 15}, Mesh -> {Range[15]}, MeshStyle -> Red, 

   AxesOrigin -> {0, 0}, PlotLabel -> t];

SeedRandom[5]; data2 = 

 Flatten[Table[{x, y, RandomReal[]}, {x, 7}, {y, 7}], 1];

f2 = Interpolation[data2, Method -> "Spline"];

g2 = Interpolation[data2, Method -> "Hermite"];

drawfun2[f_, t_] := 

 Plot3D[f[x, y], {x, 1, 7}, {y, 1, 7}, Mesh -> None, PlotPoints -> 30,

   PlotLabel -> t, 

  PlotStyle -> Directive[Orange, Specularity[White, 50]]]

GraphicsGrid[{{drawfun[f, "Spline method"], 

   drawfun[g, "Hermite method"]}, {drawfun2[f2, "Spline method"], 

   drawfun2[g2, "Hermite method"]}}, ImageSize -> {500, 500}]
Out[1]=