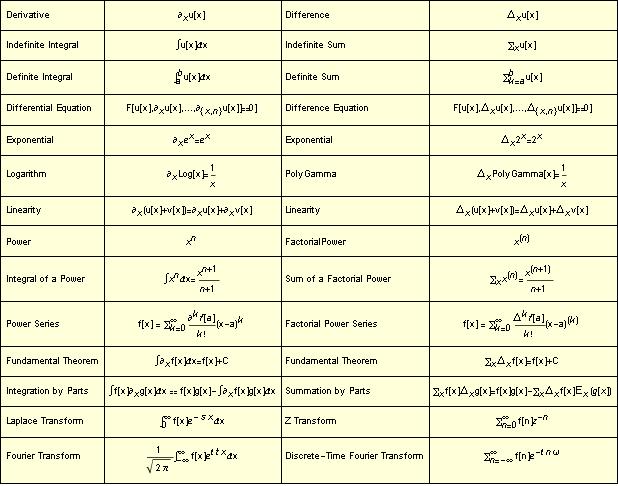
grid = Grid[{
{"Derivative", "\!\(\*SubscriptBox[\"\[PartialD]\", \"x\"]\)u[x]",
"Difference",
"\!\(\*SubscriptBox[\"\[DifferenceDelta]\", \"x\"]\)u[x]"},
{"Indefinite Integral", "\[Integral]u[x]\[DifferentialD]x",
"Indefinite Sum", "\!\(\*SubscriptBox[\"\[Sum]\", \"x\"]\)u[x]"},
{"Definite Integral",
"\!\(\*SubsuperscriptBox[\"\[Integral]\", \"a\", \"b\"]\)u[x]\
\[DifferentialD]x", "Definite Sum",
"\!\(\*UnderoverscriptBox[\"\[Sum]\",
RowBox[{\"k\", \"=\", \"a\"}], \"b\"]\)u[x]"}, {"Differential \
Equation",
"F[u[x],\!\(\*SubscriptBox[\"\[PartialD]\", \"x\"]\)u[x],\
\[Ellipsis],\!\(\*SubscriptBox[\"\[PartialD]\",
RowBox[{\"{\",
RowBox[{\"x\", \",\", \"n\"}], \"}\"}]]\)u[x]]\[Equal]0]",
"Difference Equation",
"F[u[x],\!\(\*SubscriptBox[\"\[DifferenceDelta]\", \"x\"]\)u[x],\
\[Ellipsis],\!\(\*SubscriptBox[\"\[DifferenceDelta]\",
RowBox[{\"{\",
RowBox[{\"x\", \",\", \"n\"}], \"}\"}]]\)u[x]]\[Equal]0]"},
{"Exponential",
"\!\(\*SubscriptBox[\"\[PartialD]\", \
\"x\"]\)\!\(\*SuperscriptBox[\"\[ExponentialE]\", \
\"x\"]\)=\!\(\*SuperscriptBox[\"\[ExponentialE]\", \"x\"]\)",
"Exponential",
"\!\(\*SubscriptBox[\"\[DifferenceDelta]\", \
\"x\"]\)\!\(\*SuperscriptBox[\"2\", \"x\"]\)=\!\(\*SuperscriptBox[\"2\
\", \"x\"]\)"},
{"Logarithm",
"\!\(\*SubscriptBox[\"\[PartialD]\", \
\"x\"]\)Log[x]=\!\(\*FractionBox[\"1\", \"x\"]\)", "PolyGamma",
"\!\(\*SubscriptBox[\"\[DifferenceDelta]\", \
\"x\"]\)PolyGamma[x]=\!\(\*FractionBox[\"1\", \"x\"]\)"}, \
{"Linearity",
"\!\(\*SubscriptBox[\"\[PartialD]\", \
\"x\"]\)(u[x]+v[x])=\!\(\*SubscriptBox[\"\[PartialD]\", \"x\"]\)u[x]+\
\!\(\*SubscriptBox[\"\[PartialD]\", \"x\"]\)v[x]", "Linearity",
"\!\(\*SubscriptBox[\"\[DifferenceDelta]\", \"x\"]\)(u[x]+v[x])=\
\!\(\*SubscriptBox[\"\[DifferenceDelta]\", \
\"x\"]\)u[x]+\!\(\*SubscriptBox[\"\[DifferenceDelta]\", \
\"x\"]\)v[x]"},
{"Power", "\!\(\*SuperscriptBox[\"x\", \"n\"]\)",
"FactorialPower",
"\!\(\*TemplateBox[{\"x\",\"n\"},\n\"FactorialPower\"]\)"},
{"Integral of a Power",
"\[Integral]\!\(\*SuperscriptBox[\"x\", \
\"n\"]\)\[DifferentialD]x=\!\(\*FractionBox[SuperscriptBox[\"x\",
RowBox[{\"n\", \"+\", \"1\"}]],
RowBox[{\"n\", \"+\", \"1\"}]]\)", "Sum of a Factorial Power",
"\!\(\*SubscriptBox[\"\[Sum]\", \
\"x\"]\)\!\(\*TemplateBox[{\"x\",\"n\"},\n\
\"FactorialPower\"]\)=\!\(\*FractionBox[TemplateBox[{\"x\",RowBox[{\"\
n\", \"+\", \"1\"}]},\n\"FactorialPower\"],
RowBox[{\"n\", \"+\", \"1\"}]]\)"}, {"Power Series",
"f[x] = \!\(\*SubsuperscriptBox[\"\[Sum]\",
RowBox[{\"k\", \"=\", \"0\"}], \"\[Infinity]\"]\)\!\(\*FractionBox[
RowBox[{SuperscriptBox[\"\[PartialD]\", \"k\"],
RowBox[{\"f\", \"[\", \"a\", \"]\"}]}],
RowBox[{\"k\", \"!\"}]]\)(x-a\!\(\*SuperscriptBox[\")\", \"k\"]\)",
"Factorial Power Series",
"f[x] = \!\(\*SubsuperscriptBox[\"\[Sum]\",
RowBox[{\"k\", \"=\", \"0\"}], \"\[Infinity]\"]\)\!\(\*FractionBox[
RowBox[{SuperscriptBox[\"\[DifferenceDelta]\", \"k\"],
RowBox[{\"f\", \"[\", \"a\", \"]\"}]}],
RowBox[{\"k\", \"!\"}]]\)(x-a\!\(\*SuperscriptBox[\")\",
RowBox[{\"(\", \"k\", \")\"}]]\)"}, {"Fundamental Theorem",
"\[Integral]\!\(\*SubscriptBox[\"\[PartialD]\", \"x\"]\)f[x]\
\[DifferentialD]x=f[x]+C", "Fundamental Theorem",
"\!\(\*SubscriptBox[\"\[Sum]\", \"x\"]\)\!\(\*SubscriptBox[\"\
\[DifferenceDelta]\", \"x\"]\)f[x]=f[x]+C"}, {"Integration by Parts",
"\[Integral]f[x]\!\(\*SubscriptBox[\"\[PartialD]\", \
\"x\"]\)g[x]\[DifferentialD]x \[Equal] \
f[x]g[x]-\[Integral]\!\(\*SubscriptBox[\"\[PartialD]\", \
\"x\"]\)f[x]g[x]\[DifferentialD]x", "Summation by Parts",
"\!\(\*SubscriptBox[\"\[Sum]\", \
\"x\"]\)f[x]\!\(\*SubscriptBox[\"\[DifferenceDelta]\", \
\"x\"]\)g[x]=f[x]g[x]-\!\(\*SubscriptBox[\"\[Sum]\", \
\"x\"]\)\!\(\*SubscriptBox[\"\[DifferenceDelta]\", \
\"x\"]\)f[x]\!\(\*TemplateBox[{RowBox[{\"g\", \"[\", \"x\", \
\"]\"}],\"x\"},\n\"DiscreteShift2\"]\)"}, {"Laplace Transform",
"\!\(\*SubsuperscriptBox[\"\[Integral]\", \"0\", \
\"\[Infinity]\"]\)f[x]\!\(\*SuperscriptBox[\"\[ExponentialE]\",
RowBox[{
RowBox[{\"-\", \" \", \"s\"}], \" \", \"x\"}]]\)\[DifferentialD]x",
"Z Transform", "\!\(\*UnderoverscriptBox[\"\[Sum]\",
RowBox[{\"n\", \"=\", \"0\"}], \
\"\[Infinity]\"]\)f[n]\!\(\*SuperscriptBox[\"z\",
RowBox[{\"-\", \"n\"}]]\)"}, {"Fourier Transform",
"\!\(\*FractionBox[\"1\", SqrtBox[
RowBox[{\"2\", \" \", \"\[Pi]\"}]]]\)\!\(\*SubsuperscriptBox[\"\
\[Integral]\",
RowBox[{\"-\", \"\[Infinity]\"}], \
\"\[Infinity]\"]\)f[x]\!\(\*SuperscriptBox[\"\[ExponentialE]\",
RowBox[{\"\[ImaginaryI]\", \" \", \"t\", \" \", \"x\"}]]\)\
\[DifferentialD]x", "Discrete-Time Fourier Transform",
"\!\(\*UnderoverscriptBox[\"\[Sum]\",
RowBox[{\"n\", \"=\",
RowBox[{\"-\", \"\[Infinity]\"}]}], \
\"\[Infinity]\"]\)f[n]\!\(\*SuperscriptBox[\"\[ExponentialE]\",
RowBox[{
RowBox[{\"-\", \"\[ImaginaryI]\"}], \" \", \"n\", \" \", \
\"\[Omega]\"}]]\)"}},
Dividers -> All,
Alignment -> {{Left, Center, Left, Center}, Baseline},
Background -> LightYellow, Spacings -> {1, 2}, ItemSize -> Full];