| More about Mathematica » |
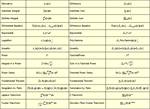
When Mathematica was first released in 1988, one of its significant achievements was the automation of traditional calculus. In a major feat of algorithmic development, Mathematica 7 now brings systematic automation to discrete calculus. Drawing on more than a century of disparate results in numerous fields, long-term R&D at Wolfram Research has led to innovations that for the first time allow coherent algorithmic treatment of discrete calculus. This achievement immediately makes possible new streamlined approaches to discrete problems in areas such as finance, actuarial science, statistics, combinatorics, algorithm analysis, information theory, numerical analysis, statistical physics, control theory and signal processing.
- Full symbolic support for any order of finite differences, ratios and shifts. »
- Major algorithms covering more than 100 new classes of symbolic sums and products.
- Support for indefinite and multivariate sums and products. »
- Symbolic solutions to many new classes of functional and difference equations. »
- New algorithms for ordinary and partial difference equations, and difference-algebraic equations.
- Optimized numerical solutions to all classes of difference equations.
- Support for ordinary and exponential generating functions, including multivariate. »
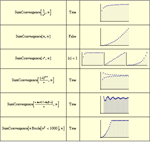
- Fully multivariate Z transform, discrete-time Fourier transform and Dirichlet transform. »
- New discrete convolution, Dirichlet convolution and divisor sum functions. »
- New symbolic continued fraction operator. »
- Function for determining symbolic conditions for convergence of a sum. »
- Complete support for general holonomic sequences, including systematic identity proving.
- Sequence recognition for finding closed forms and generating functions. »
- Support for Abel, Borel, Cesaro and other regularization methods for divergent sums. »
- Full support for q-functions throughout discrete calculus. »
- Casoratian linear independence testing. »
- Direct support for visualization of discrete functions. »