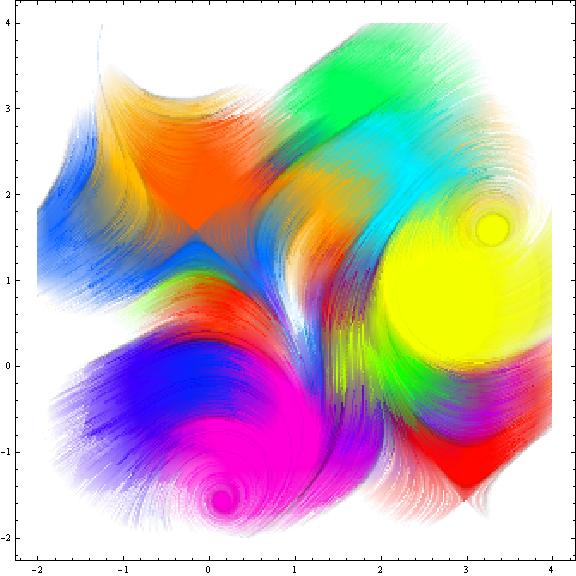
LineIntegralConvolutionPlot[{{Cos[y] - Sin[x]^3, -.1 y - 

    Sin[x]}, \!\(\*

GraphicsBox[{

{Hue[0.8561885876899418], EdgeForm[GrayLevel[0]], 

       DiskBox[{2.2300526777858103`, 0.10923569499762209`}, 

        0.8666278508201009]}, 

{Hue[0.059403037520158186`], EdgeForm[GrayLevel[0]], 

       DiskBox[{3.4039863165305624`, 1.7842464049243647`}, 

        0.6950735789471831]}, 

{Hue[0.004636367830086696], EdgeForm[GrayLevel[0]], 

       DiskBox[{3.8667340456567594`, 0.38118232952241726`}, 

        0.9728388475304066]}, 

{Hue[0.9993686860145388], EdgeForm[GrayLevel[0]], 

       DiskBox[{2.7452628752893666`, 2.0932736105500087`}, 

        0.6614396763951884]}, 

{Hue[0.7235561054336119], EdgeForm[GrayLevel[0]], 

       DiskBox[{2.0059792921209603`, 3.082647913022238}, 

        0.3707157283983613]}, 

{Hue[0.11902467326875765`], EdgeForm[GrayLevel[0]], 

       DiskBox[{3.4201613613535438`, 2.937168397770133}, 

        0.9757814426323912]}, 

{Hue[0.5028074430695157], EdgeForm[GrayLevel[0]], 

       DiskBox[{0.7010103127677061, 0.5013258667755158}, 

        0.3684123312399108]}, 

{Hue[0.24433454930926635`], EdgeForm[GrayLevel[0]], 

       DiskBox[{0.8316677421556316, 2.4800234334522324`}, 

        0.636431167705152]}, 

{Hue[0.78545678376215], EdgeForm[GrayLevel[0]], 

       DiskBox[{3.9565097920147245`, 0.5179187191830836}, 

        0.5630150525782867]}, 

{Hue[0.9881505441216214], EdgeForm[GrayLevel[0]], 

       DiskBox[{3.6260582602217264`, 2.058392628576372}, 

        0.8301197963799036]}, 

{Hue[0.8776945988312024], EdgeForm[GrayLevel[0]], 

       DiskBox[{0.2796155621960983, 1.0042811055446288`}, 

        0.05902280321410314]}, 

{Hue[0.8792810143007761], EdgeForm[GrayLevel[0]], 

       DiskBox[{0.8647091566117453, 0.8233595373391172}, 

        0.3470557771689151]}, 

{Hue[0.4519257435622708], EdgeForm[GrayLevel[0]], 

       DiskBox[{0.8345657158996254, 3.1580970879759853`}, 

        0.3152274620476847]}, 

{Hue[0.10200725975105263`], EdgeForm[GrayLevel[0]], 

       DiskBox[{2.8326974457764953`, 0.767249155679802}, 

        0.4032830865302266]}, 

{Hue[0.39337616519712326`], EdgeForm[GrayLevel[0]], 

       DiskBox[{2.8835188244374237`, 3.711694424261786}, 

        0.9226005602569463]}, 

{Hue[0.7294714326154526], EdgeForm[GrayLevel[0]], 

       DiskBox[{2.998159615709522, 0.8136165455353908}, 

        0.9152240363708277]}, 

{Hue[0.5127992809422153], EdgeForm[GrayLevel[0]], 

       DiskBox[{3.200871413523233, 2.8666477741226597`}, 

        0.9599282810006498]}, 

{Hue[0.25677783113734765`], EdgeForm[GrayLevel[0]], 

       DiskBox[{0.7303640820195767, 1.767136503865565}, 

        0.34056302896793134`]}, 

{Hue[0.2422151926083722], EdgeForm[GrayLevel[0]], 

       DiskBox[{0.4960786733797251, 2.772959771246197}, 

        0.011462057142973547`]}, 

{Hue[0.5764333736990115], EdgeForm[GrayLevel[0]], 

       DiskBox[{2.32337489978595, 0.8459525316566294}, 

        0.43233129852750496`]}, 

{Hue[0.11293504031439672`], EdgeForm[GrayLevel[0]], 

       DiskBox[{2.32903991473684, 2.713195561524734}, 

        0.5962138842373113]}, 

{Hue[0.7214905201935407], EdgeForm[GrayLevel[0]], 

       DiskBox[{2.210855926070499, 0.3738944436007454}, 

        0.3964233768909806]}, 

{Hue[0.7624636014006425], EdgeForm[GrayLevel[0]], 

       DiskBox[{1.4057090847995415`, 1.6157379926683824`}, 

        0.4543047637542035]}, 

{Hue[0.6075465005089298], EdgeForm[GrayLevel[0]], 

       DiskBox[{0.07021551480982069, 2.637732133114871}, 

        0.9278595777566316]}, 

{Hue[0.024203519091824832`], EdgeForm[GrayLevel[0]], 

       DiskBox[{1.197001647617288, 1.4041718854242067`}, 

        0.5323825218688323]}, 

{Hue[0.24333407252656358`], EdgeForm[GrayLevel[0]], 

       DiskBox[{3.2458695390625776`, 1.0508988895986207`}, 

        0.3896195191383254]}, 

{Hue[0.3398974819238383], EdgeForm[GrayLevel[0]], 

       DiskBox[{3.402761529453584, 0.8673768769534735}, 

        0.6333011979405183]}, 

{Hue[0.12033856464925896`], EdgeForm[GrayLevel[0]], 

       DiskBox[{0.534956397755554, 3.0995475105165706`}, 

        0.8809637685464964]}, 

{Hue[0.10983889880887476`], EdgeForm[GrayLevel[0]], 

       DiskBox[{1.2473820370323283`, 3.2970541263394972`}, 

        0.30291939901295484`]}, 

{Hue[0.20955035172013625`], EdgeForm[GrayLevel[0]], 

       DiskBox[{2.7951797561395626`, 1.01303118995666}, 

        0.45734471626175477`]}, 

{Hue[0.7503883913212641], EdgeForm[GrayLevel[0]], 

       DiskBox[{2.254746631456392, 1.7569662273344582`}, 

        0.12658333871684113`]}, 

{Hue[0.8852670413412478], EdgeForm[GrayLevel[0]], 

       DiskBox[{0.17642999003983562`, 2.2732380770435583`}, 

        0.03826494986036755]}, 

{Hue[0.7106296683745943], EdgeForm[GrayLevel[0]], 

       DiskBox[{0.4777956073854117, 0.3356702124170621}, 

        0.8723734357195487]}, 

{Hue[0.6007537554960771], EdgeForm[GrayLevel[0]], 

       DiskBox[{1.9844056905714096`, 3.3503793850621317`}, 

        0.08420902843236688]}, 

{Hue[0.17384041707616382`], EdgeForm[GrayLevel[0]], 

       DiskBox[{3.9387525664221634`, 1.7503730823302188`}, 

        0.9890522029033209]}, 

{Hue[0.5846105941264284], EdgeForm[GrayLevel[0]], 

       DiskBox[{1.4574929872110278`, 2.264567570700767}, 

        0.519729956518683]}, 

{Hue[0.859178096798858], EdgeForm[GrayLevel[0]], 

       DiskBox[{1.4785382061907555`, 0.04810787380248449}, 

        0.9707805278234636]}, 

{Hue[0.6413200876182676], EdgeForm[GrayLevel[0]], 

       DiskBox[{0.9580702862141246, 0.6783752352068335}, 

        0.47048829146252524`]}, 

{Hue[0.05836364444004016], EdgeForm[GrayLevel[0]], 

       DiskBox[{1.0376181417210493`, 3.027018628903485}, 

        0.7568076827944887]}, 

{Hue[0.43985130803725214`], EdgeForm[GrayLevel[0]], 

       DiskBox[{3.3516819756149383`, 2.8407182839537235`}, 

        0.04392772983613513]}},

ImageSize->{101., Automatic}]\)}, {x, -2, 4}, {y, -2, 4}, 

 LineIntegralConvolutionScale -> 0.6, RasterSize -> 300, 

 ImageSize -> Large]