Sciences de la vie
Utilisez System Modeler pour la modélisation et l’analyse tout au long de la découverte, du développement, des essais cliniques et de la fabrication de médicaments. Cet environnement flexible prend en charge des domaines d’application tels que la biologie des systèmes, la bioinformatique, etc.
Incertitudes liées à l’immunité collective
L’étude de la dynamique du modèle SIR (sain-infecté-guéri) est essentielle pour lutter contre les pandémies. Tout commence par le concept bien connu de R0, le taux de reproduction, qui mesure la contagion de la maladie. L’analyse de R0, y compris ses modèles de répartition potentielle tels que le modèle gaussien ou uniforme, joue un rôle important dans l’élaboration de réponses efficaces pour la santé publique, de stratégies de vaccination et d’élaboration de politiques.
Modélisation de la dynamique des populations saines-infectées-guéries
Le modèle SIR offre des informations utiles sur l’immunité de groupe, illustrant l’équilibre complexe entre les populations saines, infectées et guéries dans le cadre d’un programme de vaccination.

Le modèle SIR présente le flux de progression de la maladie avec la vaccination, montrant les transitions passant de sain à infecté puis à guéri, les vaccinations permettant une guérison directe sans infection.
Changements dans les tendances épidémiques
Examinons une représentation détaillée des variations des populations saines, infectées et guéries sur 200 jours avec un taux de vaccination quotidien de 0,5 %. Cette analyse visuelle est essentielle pour retracer le cours d’une épidémie, fournir une perspective claire sur l’efficacité des mesures sanitaires actuelles et souligner la nécessité de stratégies adaptatives.
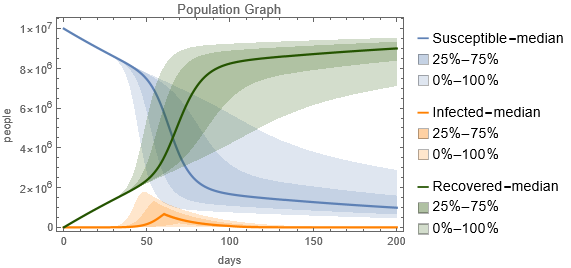
Une simulation du modèle SIR avec une incertitude uniformément répartie de 20 % dans le R0 décrit la médiane et la gamme des individus sains, infectés et guéris au fil du temps. Comme on le voit, l’heure et la date du pic d’infection des individus dépendent fortement du R0.

Exécutez facilement une analyse d’incertitude à l’aide de la fonction SystemModelUncertaintyPlot.
Étude des incertitudes distribuées selon une loi gaussienne dans le système
Parallèlement au R0, la durée moyenne de la contagion joue un rôle crucial dans la dynamique de l’immunité de groupe. Dans ce cas, les incertitudes sont supposées suivre une loi gaussienne, avec une variance de 20 % à la fois dans le nombre de reproduction et dans la période moyenne de contagion.
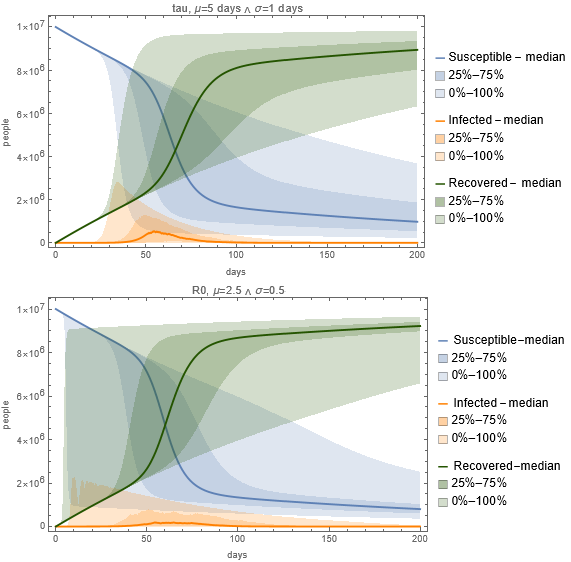
Courbes épidémiques avec le graphe supérieur modélisant une durée moyenne d’infection de 5 jours et une variance de 1 jour, et le graphe inférieur avec un R0 moyen de 2,5 et une variance de 0,5, révélant différentes dynamiques de propagation de la maladie.
Efficacité des vaccins et limites des soins de santé
L’utilisation de la fonction SystemModelUncertaintyPlot pour analyser l’incertitude liée à l’efficacité des vaccins est essentielle pour une sélection optimale des vaccins et une allocation optimale des ressources. Cette approche souligne l’impact vital de l’efficacité des vaccins et de la capacité des soins de santé sur la gestion des infections.

L’influence d’une incertitude de 20 % sur l’efficacité des vaccins et l’utilisation des capacités de soins de santé suggère qu’il est probable que les capacités de soins de santé ne répondront pas à la demande.
Wolfram System Modeler
Essayez
Achetez
System Modeler est disponible en anglais
et en japonais
sur Windows, macOS et Linux »
Vous avez des questions ou des commentaires ? Contactez un expert Wolfram »