Find Optimal 3D Print Orientations

With a broad support for mesh-based geometric regions, printability analysis from structural loads to upright orientation is easy to perform.

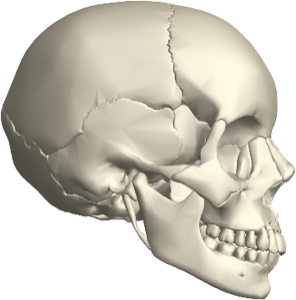
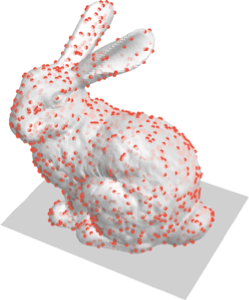
Find candidate orientations for placing the model on a flat surface.

In[1]:=

cover = TransformedRegion[ MeshRegion[ Import["http://www.thingiverse.com/download:342676", "STL"], PlotTheme -> "Minimal"], TransformationFunction[{{1., 0.5, 0.03, -0.06}, {-0.05, 0.03, 1.1, 0.1}, {0.53, -1.02, 0.05, 0.19}, {0, 0, 0, 1.}}]]; points = MeshCoordinates[cover]; transform[Polygon[points_]] := Module[{proj = points}, proj[[All, 3]] = 0; Last[FindGeometricTransform[proj, points]]]; highlight[convexHull_, cover_] := Show[HighlightMesh[ convexHull, {Style[1, Brown], Style[2, Opacity[0.3, Brown]]}], cover]; Show[cover, Boxed -> True]

Out[1]=

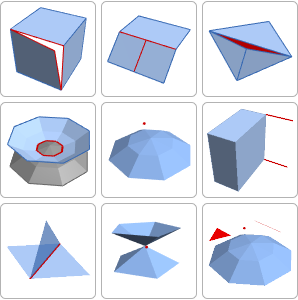
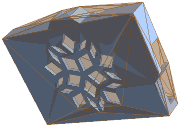
Each face of the convex hull represents a candidate orientation.

In[2]:=

convexHull = ConvexHullMesh[points]; orientations = MeshPrimitives[convexHull, 2]; highlight[convexHull, cover]

Out[2]=

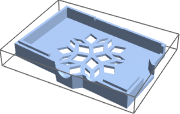
Use the orthogonal projection of the center of mass to further restrict candidate orientations.

In[3]:=

masscenter = RegionCentroid[cover]; projection[polygon_, p_] := RegionNearest[AffineSpace @@ polygon, p]; candidates = Select[orientations, RegionMember[#, projection[#, masscenter]] &];

A candidate orientation.

In[4]:=

Show[ncover = TransformedRegion[cover, transform[Last[SortBy[candidates, Area]]]], Boxed -> True]

Out[4]=

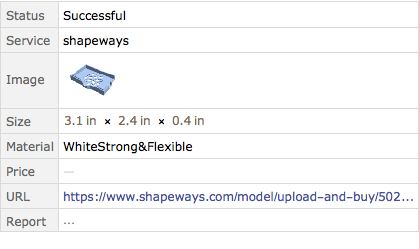
Print the model.

In[5]:=

Printout3D[ncover, "Shapeways"]

Out[5]=