Untersuchen Sie die Bildung einer Stoßwelle

Verwenden Sie die viskose Burgersgleichung, um die Bildung einer Stoßwelle zu untersuchen.

In[1]:=

BurgersEquation = \[PartialD]u(x, t)/\[PartialD]t + u(x, t) \[PartialD]u(x, t)/\[PartialD]x == \[Epsilon] \[PartialD]^2u(x, t)/\[PartialD]x^2;

Schreiben Sie eine stückweise Anfangsbedingung vor.

In[2]:=

InitialCondition = u[x, 0] == Piecewise[{{1, x < 0}}];

Lösen Sie das Anfangswertproblem.

In[3]:=

dsol = DSolveValue[{BurgersEquation, InitialCondition}, u[x, t], {x, t}]

Out[3]=

Die Lösung ist für jeden beliebigen positiven Wert von ϵ geglättet.

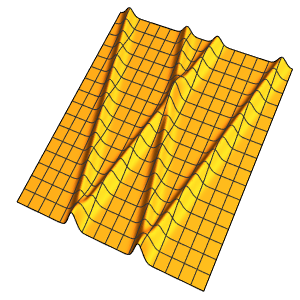
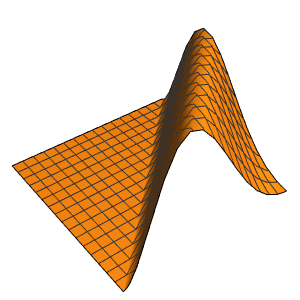
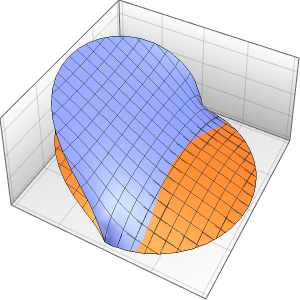
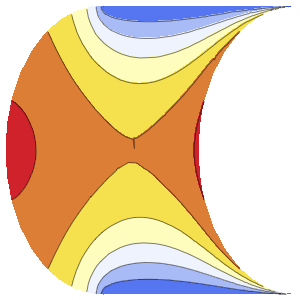
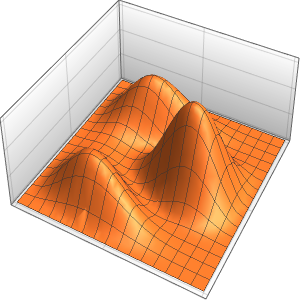
In[4]:=

Plot3D[dsol /. {\[Epsilon] -> 1/10}, {x, -2, 2}, {t, 0.001, 5}]

Out[4]=

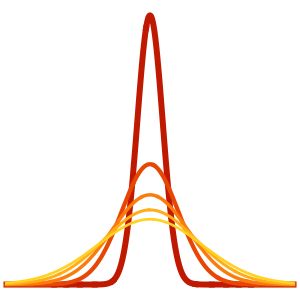
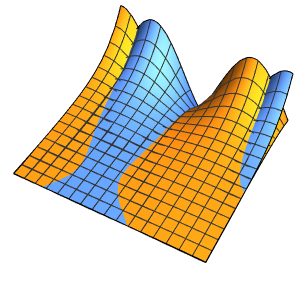
Die Lösung entwickelt eine Diskontinuität am Grenzwert, wenn sich ϵ 0 nähert.

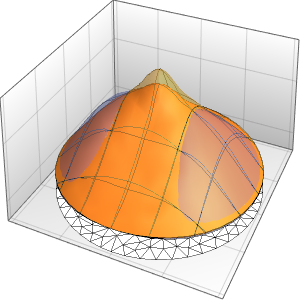
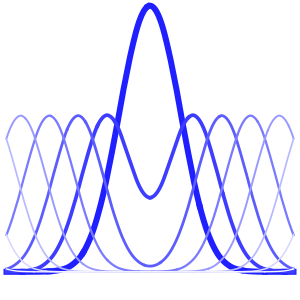
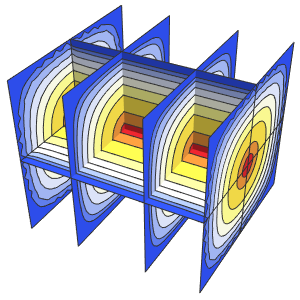
In[5]:=

Row[Table[Plot3D[dsol, {x, -2, 2}, {t, 0.001, 5}, Exclusions -> None, Ticks -> None], {\[Epsilon], {1/10, 1/100, 1/1000}}]]

Out[5]=

Bestimmen Sie den Wert einer europäischen Kaufoption bei einem Basiswert und einem Ausübungspreis von 100 $, einem risikofreien Zinssatz von 6%, einer Volatilität des Basiswerts von 20%, und einer Optionslaufzeit von 1 Jahr. Verwenden Sie dazu das Black–Scholes-Modells.

In[6]:=

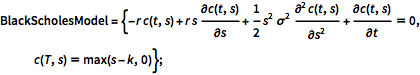
BlackScholesModel = {-r c(t, s) + r s \[PartialD]c(t, s)/\[PartialD]s + 1/2 s^2 \[Sigma]^2 \[PartialD]^2c(t, s)/\[PartialD]s^2 + \[PartialD]c(t, s)/\[PartialD]t == 0, c(T, s) == max(s - k, 0)};

Lösen Sie das Anfangswertproblem.

In[7]:=

(dsol = c[t, s] /. DSolve[BlackScholesModel, c[t, s], {t, s}][[ 1]]) // TraditionalForm

Out[7]//TraditionalForm=

Berechnen Sie den Wert der europäischen Kaufoption.

In[8]:=

dsol /. {t -> 0, s -> 100, k -> 100, \[Sigma] -> 0.2, T -> 1, r -> 0.06}

Out[8]=

Vergleichen Sie diesen mit dem von FinancialDerivative berechneten Wert.

In[9]:=

FinancialDerivative[{"European", "Call"}, {"StrikePrice" -> 100.00, "Expiration" -> 1}, {"InterestRate" -> 0.06, "Volatility" -> 0.2 , "CurrentPrice" -> 100}]

Out[9]=