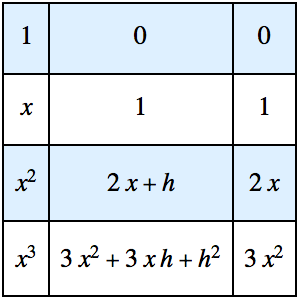
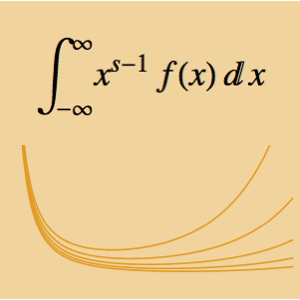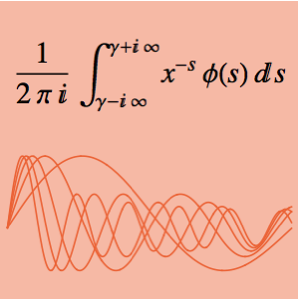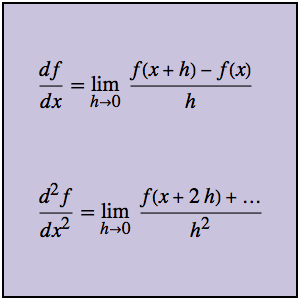그린 함수를 사용한 경계값 문제 해결
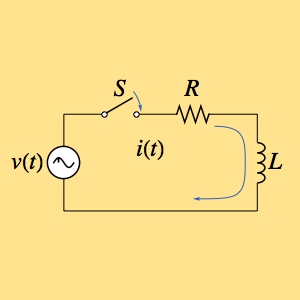
지정된 동질 경계 조건의 대상이 되는 다음의 2계 미분 방정식을 풉니다.
In[1]:=
eqn = -u''[x] - u'[x] + 6 u[x] == f[x];In[2]:=
bc0 = u[0] == 0;In[3]:=
bc1 = u[1] == 0;강제 조항은 다음의 함수 f[x]에 의해 주어집니다.
In[4]:=
f[x_] := E^(-a x)해당 미분 연산자에 대한 그린 함수를 계산합니다.
In[5]:=
gf[y_, x_] = GreenFunction[{eqn[[1]], bc0, bc1}, u[x], {x, 0, 1}, y]Out[5]=
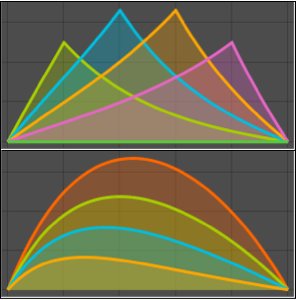
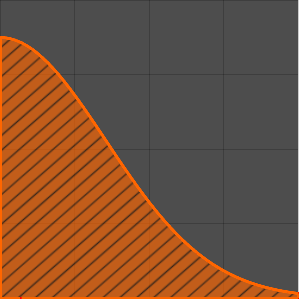
0에서 1사이의  의 다양한 값에 대한 그린 함수를 플롯합니다.
의 다양한 값에 대한 그린 함수를 플롯합니다.
In[6]:=
Plot[Table[gf[y, x], {y, 0, 1, 0.2}] // Evaluate, {x, 0, 1}]Out[6]=

지정된 강제 조항을 가진 오리지널 미분 방정식의 해는 구간  에서 합성곱 적분을 사용하여 계산할 수 있게됩니다.
에서 합성곱 적분을 사용하여 계산할 수 있게됩니다.
In[7]:=
sol = Integrate[gf[y, x] f[y], {y, 0, 1}, Assumptions -> 0 < x < 1] //
SimplifyOut[7]=
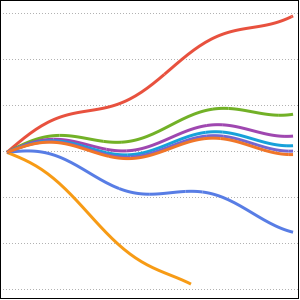
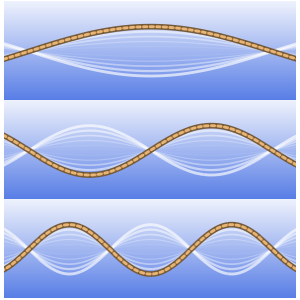
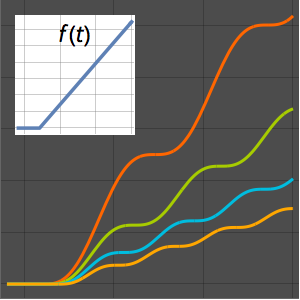
매개 변수  의 다양한 값에 대한 솔루션을 플롯합니다.
의 다양한 값에 대한 솔루션을 플롯합니다.
In[8]:=
Plot[Table[sol, {a, {1/4, 1, 2, 4}}] // Evaluate, {x, 0, 1}]Out[8]=