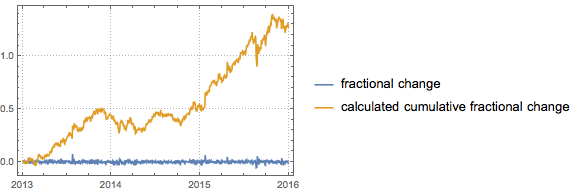
Cumulative Fractional Change
Compute the cumulative fractional change for the SBUX stock price for 2015 from the corresponding time series of fractional change of SBUX stock price.
show complete Wolfram Language input
In[2]:=
ts = TemporalData[TimeSeries, {CompressedData["
1:eJw9Vwk0lV243oYifyIkSaWBUJlS8Zf2yZTUQWQOxxwajJnZ5nkeMhUVihAZ
kmifSsVfEaUiiaJoIkWi4b7ddddtrRbrHN/+9n7eZ9pr7U8YOXEihDjg/9e/
v9wJj1ycEoRR0eF9fJV+GOXuWGZwYQ9Ggl6u9S7WdCjg5/45tQyKlgQmcv22
pKRFJom/LByjiC1yXw0DKGIlKNj5H6VoxdMB5SQHis6FC30ucMboi22ewwFY
z824WP2dG2aMS26Ta42kSPEdz/tEFh7i2MPQ5i7FbA9y/2ZgEiU8wTfiGkIp
2j4x3ugXglHlEa63yXYYGZlw63EkYlTzevPH64kUre3cX+0D6/5i7T760oki
i8+i823uFCUcb7h2JQKTbrUAx0YPiu4GudVG2GGy/BY11A+jKLx550CCD2Wt
P352qX4ORT0DOprZLMyu4tI54pFNkYzqropsXYzK0l+5B6ZiQnbwX5WCc9cc
97uVbILZlRmtM//lYlRhfm83ty9G6Erb3tEdGCnZht+cS8HoiKK6dnsyRot2
6b6zi8bIQWWyoCgLI1LOjoyD85gnLlW/aUhRUsTMjIAfRZwreNI7YJ2kwjTB
rlSKxmwvbri2nRLrOvOGT/EUVe9IZ907/HefmoZF0Zj0JHAriwfBPjMKPGv9
MPkurlpaHEfR4vOtDzkDMbo4+vSwuCNFhu2+Mrx7MVoXos3NbUbRotXDmCcP
MziDrAMvA/6y60ZfiMN+BLwinvf5Ai6ynnuqTsL+KuNuc8N7nbOeMR4DH5Zk
JSueB9yflDZ7PQnH5JKC8Kb3pyiK0/eXlUvB5LOwr8veIEqa1i+puhxGSfyl
V+cl44BHjkfkez0wkgk1LFBKwGjrt99p5qGYHMqLlpuIweh5CPn2kQCu6Qcl
H0RiVMJedDDLEzP0+o0YabEUST9UyjL3wIx2U/FPWnkYFd+f3KgUhdHhYKWg
xSYUGakxBueOYpQlXVDH0KNIcGI1YcJ7o3y7JjZ7UaSbWC7RE4NJw6eYC9fD
MVs3eEqxCN7ncTpnrgb40Rh2SU7Wm6It0VHZXwG3zwNrZsIsKGrovTYmEUXR
VeV1nucAR562VdrLkzF7oewiERH4fJTrDSvPkZKdhf7v9gNu5f0JzFs+GLVi
64XtLEpK/vszyZFG0T2l0NemMZglf/CtnmsxZsSf1St9nobJYdv05axoijZP
X7pjnULZ9qwnftK5mGjxGq76cZIiCTq7rw/280tv09ypNMxICCnSE4imrJ3W
StYWGZRxIaY/pgTOYVhzXjoW1ukWH1e0isVsDsKQbkvDSF6E0ehgRdGJ3bfj
vJwp8dO+ogs4oOBf2RocoNf7Rc3PdcIw+jF/vTM1ABNvluHELvjc0DMoVwl0
q1ivIPliF0WPnDh3l2ZgJMo/GOsFvJD599yY8gE4741VX0/COeX5zN09Myn6
bc4j2g1zFizSvpnghVHoY75yB3c8pHFf2GZLFiX6E57G7amULNIUs5s/hRmz
vkZ+IXWY8dHcL9cFeHZ/4ey0UwhlD4QYDKpGUJTb8WfGpwijueEHpu9g3jL6
gwW14CtWcq2XLyRQdvubpKWy4RTNv8RTOqAvHWMPNy9biswtN5/bY40JPVad
vg90r9hV/1E7hjKYe0PLzoOumiL6BO7vpMg3TU/jkD9F+q8iLqWC7jxejikq
gE6WcSo07kzHyH+UzL81wKj5eYVpyCGKfk1W3iK5FIkKvd9kGQvfM7NfOLli
9vaXcpa/YL8TgZdsrFMx0r4Voz0SCr75pDHUA567gO2u7ANd8G/et3M0DrP7
eVVcZfMw6RTc5r4B5sQ3VNB/9Dic0zO2s8yEEuMixZnXnhR1mb7Ovgs6rxNp
3G6bjkmTvYX+N8DpQ3i1W9URSlbynj3rFUXZPsYSwZtgnfSxSJ0AZ4pqlx78
EQdznl0/8PiZLSb/LslKWAr8HvMTG1V1xIghsL0wUA0jXR+zX3OAj0hDR7l6
MEZ3J4+UZwbToe6j00pN6cDvo3oluscoaatvatQH3T2uPtCVEwG+YNxzPuAY
ZvgzRVMhB9iKYtcFbwJeQhdXXbOB7+/pZJaWgZ8k9cZ1/LQBXQpWVaRkYPKc
lmVFRVPGdLh0eHY8JaIenscyga/RJan8nKATYcEXyVWA65X54do1gCOyMJnf
74zZOsIqzfIw5//9V9zC4Hi0duZ8Fmb7Z+/eHwR66EQF8igf+O9XXZ5dgNGg
Y2+pAuSA40+nYEtzigqb8pxyAcc3PRvWLIfzzsYKpilpYUZ1ro2bE+indVcu
VxzkwZqvwuqZLhTNpZxhl5zCSERyi6CoPSU/jvPWShBKFr5Qbj8APCxxWMaU
MMWobqmLpADwv33lgHIh4LvkeXSLdiAlRxLeMa8kUHTRQ9LvEuRemvdq77/5
FyypvDHaiRKuwoWZ8mco8ulZMTMB8+R1ExGWOYhRfoP8zT7Qa8kLnel8M0yk
XD/t7PGm7PuS6IVTNiabadveKfD7nsS8YmHw48uGI9UuoNcyZQF5aTeMVhAt
WVnQn8mOb2/F4JxIvvdulSLg+vrOi8ssylavHCl8Bfx/8uBijaULJS4NYW63
wMeaI5YFzICvZxH19WzAKdLilHMG+E+c1JrvKUzM2PSzc3dXMfjAe/738aDr
Pc+V5roiMfvZqgxFJcgbdIKZv8OXMh64NL4VBd4Qmr8E61Ck3SHYZAvvmay0
tlfIweTx8s0yvNGUjM53J5R70mLRoyekpGBdE079y7zgm1ZWuZ1hMZSdqrHy
3jfA57jNo4TxQugLfILhyfYUfeIXMZIrwETQu1rjLsxn57hp1QLQ/aSFXsox
OO/S3RuXqP71Q7cBjtPwuZnhdrVSL8xYt77n2+ckyjhqliHxB3hk/m9m0xVX
jIQleZelJ/4frxBiHVj+pdq6kJIbx4MP9gOfLcc+uTlBrj4b0Yr2gnMNTgVc
0Q2m5L5j3HU90GPRGVua6UMJt+jXiJlMjEZpSq4r+MiW+dxCP5iPTM9IwUnI
+81mX86wCC7eq/7bCgPPDTZ37i+0g5zupUf7jaEfra8dV4T+Eq8bbjkP772Y
qsRxKAmjvdnugYVulOSqBhWIxVPGx4J9KZYwv9YOOmmTDD42ytWiCH6nHih9
odUD+sCeE73t4BsXPG/szQZe/Gx/KtcN+WcZsrFhDaFDxcHrTDKzqeTIBX9v
njTI523Sh+Kgp9Rb6N8sS8KsB3TDx09FlNh+FT/RDP0H4b3GupDzxm7Rgj3g
k6KfNH6rF2JGWrDSr0jwu9HfflTLGyMfZsC8H+S2qlWj9hDMt79uwUNr0EnS
5UmuGzBX2hbO7AqhaLh8bAOFOdW87ziYrAy+vKxIGIVgMrz7UO8UfE+mX91I
84JeEWvtzoRz9su90Hxqj9FVg6tb74MOxQLPDo5GYfJFIu7SknjwMcFZm2Pr
MPo4tmNFaBJFqzPtXlXBeQOfv/SfBv9gfPc9F2CEGTEW+ybuxVAkOZru+MQB
/PCeswbkOBHK4PpyjmDGoiVWTm9PYdLR93DkMuR47ESM35u/88k4OrcWcqQ+
XqhmCeD54/ShHCbw/7vKIoclMF/D/LTsL9qYWPMtVG4iGLWU/PxpAH4wX8dX
mAd+8pT3n/QZJ5jjj5e3/8D7zz48ObAdcPE/xR83ATyJu+ymiY7AOsLD15Xc
MUPgTknvWdDJt4721/Xkb2/ZGt1phcmK4eNcl8FXrQVjljHgp8o9TqdN+yia
aVufqQA9xZ7NL348BHjrXTcUA9+r7o3nWQb+UT3IzumA3jN3fa/WJvCnwFtD
3kutKBHKET69NRaT/uGqls/Qr0vV1yj8cKWILbVQqooB/Oy8VqviidF4Z+rO
03CeTFn2NrtMSgzsjgakQl8y2BdQbwY8m1MMz+uGfvvsgF5npw9mf0/v3v01
DbNluW7O3wb+nDMbd2iD92o1KWgehHxrqs9bzge9303deaAC5lss/jTKB3hU
neLRpAk8kOwKvuoJ94cJsY6qdYDzo8ltz5jgQw8n1mXuhz5XbRyWbQ8+lxaf
dItPm5JQTqWNsaGUvX/wjoMH4CXqcjCL4wQm3CsPnVgJOCyR/lg9B3N6/6Tc
cciIouTPu5jQL5B0UEHgcuhtum2LN+2Dv+uf3eY/Dv5iuPKNkp0VRhJhm6TX
mv2/LxAO1RQeW0/KHvTiFVKH/Wa7iri3AO/jWla8/A7zXHnQk/8Y5KT1Zxlp
DlgfkZaC1cbQf6oz4seBl/rLKuaDwXdYGeMNffA9r2prTg7wWkX4xUodd4wC
zX3EVYAPPg4Xyh3g3Kfv9tzsyKQMnT9nxtLhuRPJqo5PMjAraVeRvyH4x3Tr
YikuwH2XpX/lfRPoz0Gnb1Y5Ysb7rpYrS6Ev65Qfdky3o+xHtW6WnZmYHZal
tX82kjKkVzsrzYFvlHlIRFyHPjmTfuqGGvTG9tuGK/OVqKR8IJO9owjWX7bh
gUoYJirN5xO0fSjq1Cg+dOwYRgkeB17axmPycMbihzT0VxmJdZkloDfBmfk0
D5gLJ8Z9lvBTcvWT/YnQ85fwjG7Vg/tavnPL4VWw3xqf/hIJ6EHRswFvBqOw
5J6QE8IGcH/4tlm7Uxv6goR5QJYb6IgdmWBkBfP1aH7zShx8fFZR+N954GPh
1Ks2Xgc4751Yk2FDjAZev/6jZwH3gcronU8Z4DelrGpF0JPvec7VrscpSssx
em4N98CszfkfnWFffoIr1ZAPJhZUPuRYFials8KXI8G3DJrRWPwJShwrJXf8
A/nd/uSffGfwcwV/rCvjBTnJIaR5EPyvjc/8iv0hjMQ4hp+xYF+5YbYaJyGf
JvdU9CY6Y/JyS7dfN/BDJ5RVzABcMpy7tO9DX9aq8+4ussCSxhaFFjynKVvG
rOXa3hzKKAzd/hj0QnzV3hQOAc5KuoYGyqDHQrGgNqskWG/Vmbyz0OMGQ063
iLEoklettVODnta73KM2NggTtGf4PxPgkwznzlLQFel/nnDOG/TgkuPtcTqT
sj8EDCtVEMr2/Gr/fCv0twOlv1Ri0rCgSfzVDbcgd9cosqxzYH8aMzM6poB7
3HhE/38n4flaPuwIPm4pfa4nHOZYwhQY/Q19Vvf647vqBzBSt2uY0szAjGeS
RinfamB/4pHGGaCvR4/UcrwdMWkdufu0L5yyp/Vfeuqn4+LuuvK0QMjPi2LC
hTG+mHCk/9e+EXDXGUt+5AHzPFD1WK4e8Jwp+ydgN5xHsqnJM51FGdhjsfE2
6HNv98tyRYPfuIgaNPlCP+xYvNCECT3X4sK+I5Iwz8fStdw58LwYV++XKWuY
i1nL8lHgq6RLRVQs3N//Hd758JYpRQv8+FzZ4OO7nF9Kqrhiom5/tWcafPnJ
B/eP2+D8Qce/jv52oKRluHskEHrRAvl1BaIBmKEyLmLzLAXuI76X+raBX/Ry
SW/5DHO2yRoofg34ij8Y2PktG/j74nRClgEln2wUlC/Del5bTzNPwz44/xP9
45uKGboeGqWR0Aes1k+Vrge/5eZQ1tbQh/u2dPLIOj/M6rlV0R2UQ8mvHxZ1
EX/z0E4kJnMlJXRbiU8+4FXMU/LbIJEWSz3YFiaXAXi0ajTLQn7P7g84k2aK
iVfy9AYCftuVLiO9B/IxY71aVBXo6uXihkMToJ+fnHZJAsCff0LieUcgh90E
pYTXgz5GHvmiJvCje0nd51qht8pMX/kkDvP+uFXtrjDgVWgXnmKkRdmvhJR+
ip7CxX3pntEzF/FQ0p0ry2Xh3ic+HndgAvg7dttg1dt9mKQXX399Fvx/bFnn
lDHo3vTpm82CoL+b5yPXfkinjDaHk3tGIyl53aBqkAXrO4cOaD6HnqG11//b
Ij+KzkQXhrFgv36nV4bdhXnoF/0p4QHcUkZWOniC78ZPHaw7D/vrrhhaus0b
E0Yd/4KlkLf1Cj1xIv4Y2e/QPDzpgtnTqRNffeGekRq6zmE74DTdPJDoB+sm
bHTKvuoCPHp3+2so5NYFgbC8HZEUuS5+bjoM6wr/uGR2AtazGKi3L4zAbM25
OeW30NNZ+87VeMhixnCNi1RfDkaaA7EKYicoYtxvP9IHOa/7pNKfG/rhl8+H
tI9Bn+4aut47BPwcHu5qBL9Fee8f6jEAby0zm63/akCuKfj2XYW+HrVqz00e
eB/T2kfLB3Rd9mlucW8UZjua2toKZFF0wLS1xg18/gxd+k8x9CmJ8/y78wMx
4n5SsEAKPg8ujfi+ygQXb0xc4lSSQcmWqYQtB8Gna9408tYDb/hssYEK8PNR
rPkCNybwb5Vf2BrwmRrLVOUC4Ifki0X/OjEpmoyfDFoDf//IsJnHcCNFU0Wb
Nr+A+dheVOHugP41e1fs/vEETNb9yp6ShVyudJV/gABH7bVdL6IDMVFie4nm
wPO75xyvmUGeSvPnbbKHPDs3oqlfCrr9VLEm5yzkXHba0SNvoN+3XV3Lt2UP
JUbs4+vKINe4B/2/65lhxKs5ru+1B/rHYpE8IXi/YsUCKS7ohYfVmX7fwA9F
Gi0uxVtgsovJbPzjQcl5cwdWGfRWu4ROOXyJFu8ou31Y7SJFn2VStkam4KGa
pVrctysxO1lWtHf4HCYPaudVj/nRIQdbO/2JNMoQ2fyjuTSHSpY3dIw+K8bs
Rtw5swZyUfXDhel68NONI56uiemYYR/XsVgPeCtkGtd3Mh6zzWT2j3kDrmmt
Bo0O4E/ebS51KbC/OQ7Be4oBGAn+tlMf2Y7JAc0P1SfDKDl8pv6mKuiS+eD+
0Cjo23HoAntBHCZPddzfJ0OPsOxOcagIpOzxuk+38s5DbsVFJbOYlK02cUo1
G/g/LCZqIAC9zahmmA35w+Y/wvXtI/BqS+yski7kU5ya2Ic1kIcNLnIatYD3
wAe9Sk7wRfXEoo0LCSb2ge/uNARQVqEN13wn+MxD8TdVeqCL7bKdK/09MFsy
4s/6O3D/aNb5ZaQA9+anAqJGSX6UUTljckod+kK50I27ZXCPl4jPSe+BXDjM
kYtxLPTDtb+cJRPwUMU7u0Hdv3N8Y5NnYYTJIXeqme9LSQovh9ox0JGUQ9Ad
R7hvRffNk43AAyfjT9oOcH8S7dpyMhJ0gwMyav6B3GOv6G9y96FsRjB7e1AC
ZbTzePExIS+Fvkf/JwHnjf/D/S3JjjIsLOqurYd7sUzL+Mu4k5RMFS7eUQ58
GbcI9wiIxowm5qXwneDvt7JDbx+B/jn5ZjBVSIqSBLtmiQXgc6z8VTMW2yi6
5F7YtgD64LuFElOfCyg7zvKD3vtz4CPct4ozwBc3tZ2MGPTErPa8vNENcG/a
wJHDuSIWe2wQ0Z6cgRxlNbmEOEBvHCi6O+sCvSTm6jsrLZi/bX1Jhhz0P50P
m25+h/xwMVLdIgT7b2t2Xz4NPvPoqN/lUbj3KdoUC1+DfXgG5LVdsKNkb8KX
yflUuOe+Eo+6Azjw5z4RyE+g/wNF8pwH
"], {
TemporalData`DateSpecification[{2013, 1, 3}, {2015, 12, 31},
"BusinessDay", "DayRange"]}, 1, {"Continuous", 1}, {
"Discrete", 1}, 1, {
ResamplingMethod -> {"Interpolation", InterpolationOrder -> 1},
HolidayCalendar -> {"UnitedStates", "NYSE"}}}, True, 314.1];The time series is regularly sampled on business days.
In[3]:=
ts["MinimumTimeIncrement"]Out[3]=
In[4]:=
RegularlySampledQ[ts]Out[4]=
The cumulative fractional change is calculated using the following formula.
In[5]:=
fun := (Exp[Accumulate[Log[# + 1]]] - 1) &Apply the cumulative fractional change formula to the stock time series.
In[6]:=
res = fun[ts];show complete Wolfram Language input
Out[7]=