Use Databin to Store Time Series

The arrival times in a PoissonProcess are independent and follow an ExponentialDistribution. You can simulate a path of a PoissonProcess by sending signals to a Databin in time intervals specified by a simulation of an exponential distribution.

In[1]:=

SeedRandom["11"]; \[Lambda] = 0.5; times = RandomVariate[ExponentialDistribution[\[Lambda]], 30];

Create a Databin.

In[2]:=

bin = CreateDatabin[]

Out[2]=

Use the simulated times to send 1 to the databin in time intervals.

In[3]:=

Table[DatabinAdd[bin, <|"arrivals" -> 1|>]; Pause[t], {t, times}];

The recorded signal with the time stamps.

In[4]:=

TimeSeries[bin]

Out[4]=

Extract the TimeSeries object.

In[5]:=

ts1 = TimeSeries[bin]["arrivals"]

Out[5]=

This time series is irregularly sampled.

In[6]:=

RegularlySampledQ[ts1]

Out[6]=

Assume TemporalRegularity so that Accumulate does not use interpolation to resample the time series with respect to the minimum time increment.

In[7]:=

ts2 = Accumulate[TimeSeries[ts1, TemporalRegularity -> True]]

Out[7]=

In[8]:=

DateListStepPlot[ts2, Joined -> False, PlotTheme -> "Detailed"]

Out[8]=

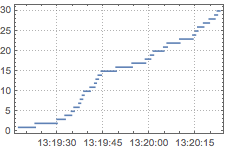
Estimate the PoissonProcess parameter from the signal and compare to the parameter of the ExponentialDistribution used to simulate time stamps.

In[9]:=

{FindProcessParameters[ts2, PoissonProcess[\[Mu]]], \[Lambda]}

Out[9]=