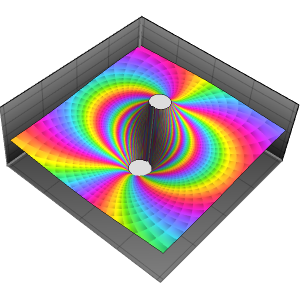
Riemann Sphere
Project the extended complex plane (http://mathworld.wolfram.com/ExtendedComplexPlane.html) onto a sphere so that the entire plane is visible, including the point at infinity.
A point 
in the complex plane is mapped to the Riemann sphere by projecting 
to the point of intersection of the sphere and the line from 
to the north pole of the sphere.
If the sphere is described parametrically as 
, 
, 
, then a point on the sphere corresponds to the point 
in the plane.
Define a function 
to project onto the sphere.
Use ComplexPlot to make a texture for the Riemann sphere using 
.
Plot the textured Riemann sphere and its equator, which is the projection of the unit circle in the complex plane.
Use ComplexPlot to make a texture for the complex plane embedded in 3-space.
Apply the complex plane texture to the 
plane.
Show the plane and sphere together. The unit circle in the plane corresponds to the equator on the sphere.
