Eigenvalues of a Structurally Damped Wave Equation
Analyze the stability of solutions of a partial differential equation by examining its eigenvalues. All eigenvalues of a stable system have negative real parts.
Compute the first 100 values of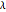 
and 
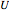such that 
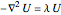on the unit disk and 
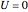on the unit circle.
Use the preceding solutions to solve the structurally damped wave equation 
with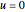 
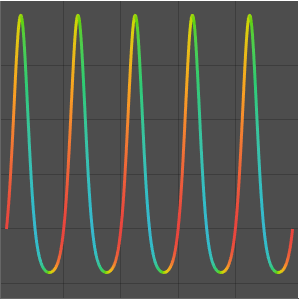
on the unit disk by looking for solutions of the form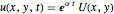 
. Smaller values of 
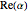correspond to solutions that decay more quickly.
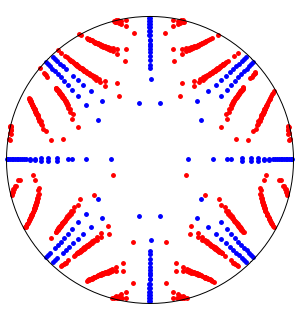
Visualize the effect of the damping parameter 
on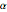 
. Values of 
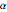accumulate at 
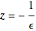, and if 
, then there are nonreal eigenvalues on the circle of radius 
centered at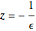 
.
show complete Wolfram Language input
