Compute Lattice Packing Densities

The "Lattice" entity domain contains useful information about classical named lattices.

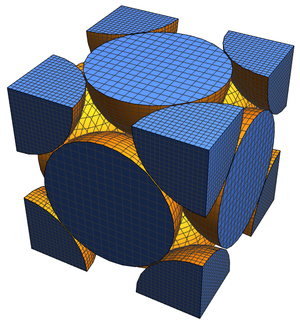
For example, consider the body-centered cubic (BCC) lattice, which can be immediately visualized using the "Image" property.

An important property of a lattice packing is the fraction of space occupied by spheres packed with the relevant configuration. For a BCC lattice, this packing density is given by the following.

In other words, spheres fill about 68% of the total space in body-centered cubic packing.

The minimal vectors generating this lattice are available as the "MinimalVectors" property.

Given these, you can make a space-filling visualization from which this density can be directly computed. Begin by constructing a list giving the centers of spheres appearing in the unit cell from the minimal vectors.

Now restrict the plot range to the region of the unit cell.

The visualization can be made slightly more elaborate by using filled balls instead of hollow ones.

As can be seen from this diagram, there are eight eighth-spheres and one full sphere in the unit cell, contributing 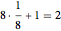full spheres. Taking 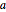as the radius of the spheres, by the Pythagorean theorem applied to a space diagonal, the overall cube has edge length 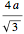, meaning the packing density of spheres is given by the expression already seen.

Now consider the face-centered cubic (FCC) lattice.

This lattice packing has a higher packing density.

That is, spheres therefore fill about 74% of the total space in face-centered cubic packing.

As before, make a space-filling visualization by first finding the centers of spheres in an FCC packing.

As can be seen from this diagram, there are eight eighth-spheres and six half-spheres in the unit cell, contributing 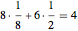full spheres. Taking 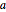as the radius of the spheres, by the Pythagorean theorem applied to a face diagonal, the overall cube has edge length 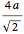, meaning the packing density of spheres is given by the expression already retrieved.

Hexagonal close packing (HCP) is another closely related packing.

It has the same packing density as face-centered cubic.

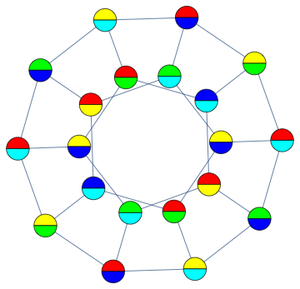
As in face-centered cubic close packing, each sphere is surrounded by 12 other spheres in HCP. Taking the Delaunay mesh of the minimal vectors for this packing is equivalent to connecting the centers of the external 12 spheres and allowing the edges to be the faces of an enclosing polyhedron.

This results in the polyhedron known as the triangular orthobicupola.