Euclid's Elements
One of the oldest and most influential mathematical treatises of all time is the Elements, a series of thirteen books by the ancient Greek mathematician Euclid of Alexandria. The constructions described in the Elements can be represented in the Wolfram Language using GeometricScene and visualized with RandomInstance.
Proposition 1 of Book I states that given any two points  and
and  , one can construct an equilateral triangle having
, one can construct an equilateral triangle having  and
and  as two of its vertices. In particular, draw two circles centered at
as two of its vertices. In particular, draw two circles centered at  and
and  , respectively, whose radii are equal to the distance between them. Then their point of intersection
, respectively, whose radii are equal to the distance between them. Then their point of intersection  forms the third vertex of such an equilateral triangle.
forms the third vertex of such an equilateral triangle.
Proposition 22 of Book I generalizes Proposition 1 by stating that for any positive quantities  ,
,  and
and  , such that
, such that  , there is a triangle having side lengths
, there is a triangle having side lengths  ,
,  and
and  .
.
Randomly choose positive quantities  ,
,  and
and  , such that
, such that  .
.
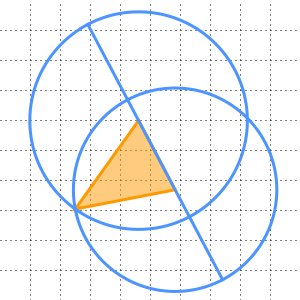
The construction proceeds as follows: construct a straight line through the points  ,
,  ,
,  and
and  in order, with
in order, with  and
and  distance
distance  apart,
apart,  and
and  distance
distance  apart and
apart and  and
and  distance
distance  apart. Draw the circle centered at
apart. Draw the circle centered at  going through
going through  , as well as the circle centered at
, as well as the circle centered at  going through
going through  . If
. If  is one of the points where these circles intersect, then
is one of the points where these circles intersect, then  is distance
is distance  from
from  ,
,  is distance
is distance  from
from  and
and  is distance
is distance  from
from  . Thus the points
. Thus the points  ,
,  and
and  form such a triangle.
form such a triangle.