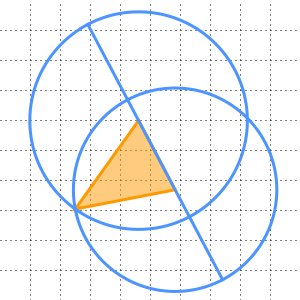
Viviani's Theorem

Viviani's theorem states that in an equilateral triangle, the sum of the distances from any interior point to the three sides is equal to the height of the triangle. Use RandomInstance to create a visual proof of Viviani's theorem.

Let be a point inside an equilateral triangle. Represent the distances from to the sides of the triangle as the heights of equilateral triangles having 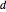as a vertex.

Extract the heights of the three smaller triangles, and note that they indeed sum to the height of the large triangle.

To see why, first rotate the upper-right equilateral triangle counterclockwise about its center, so that its height is now measured from its vertex at point .

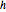
Rotate the equilateral triangle with vertices at , and counterclockwise about its center.

Now it is clear that the height of the large triangle equals the sum of the heights of the smaller triangles.