Compute Parametric Sensitivities
| In[2]:= |  X |
| In[3]:= |  X |
Perturbing a parameter in the differential equation gives a family of solutions.
| In[1]:= | 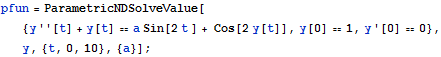 X |
| Out[2]= |  |
Sensitivity solutions clearly show the effect of small changes in the parameter.
| Out[3]= | 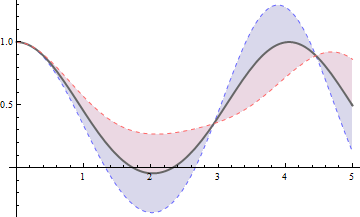 |
| « View all new features in Mathematica 9 | ◄ previous | next ► |
| In[2]:= |  X |
| In[3]:= |  X |
| In[1]:= | 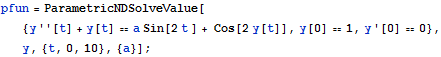 X |
| Out[2]= |  |
| Out[3]= |  |