計算生物学
生物系および生化学系をモデル化し,そのシミュレーションを実行し,可視化します.反応動力学もモデル化し,そのシミュレーションを実行します.
Herd Immunity
When a large percentage of the population becomes immune to a disease such as COVID-19, you can consider the population to be protected from the disease by herd immunity. This means that although 100% of the population may not be vaccinated, a sufficient proportion of the population is, and the rate of infection starts to decrease. In this virtual lab, you will investigate the concept of herd immunity using the SIR (susceptible, infected and recovered) model.
Model
The model used in this exercise is based on the SIR (susceptible, infected, recovered) model. This classical epidemiological model was developed by Kermack and McKendrick in the early 1900s and is one of the most well-known models for studying infectious diseases within populations. Since its development, there have been many adaptations of the model, allowing it to be used in a wide variety of settings and contexts.
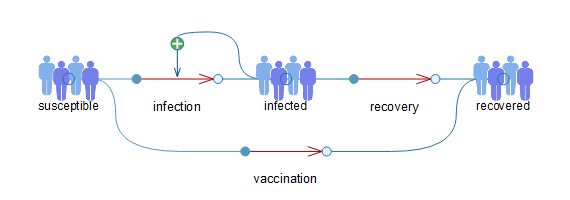
SIR model with vaccination.
Analysis
Analyze the impact of infection for different basic reproduction number (R0) values and mean infectious period. To model the influence of COVID-19, set the R0 value to 2.65 and the mean infectious period to 5 days.
Analysis
Use the Wolfram Language to carry out parametric analysis.
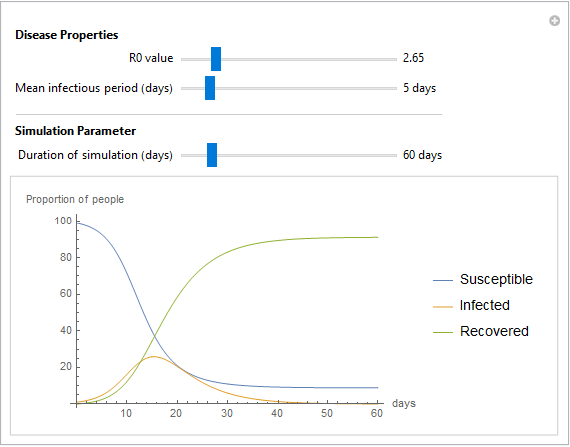
Dynamic visualization of spread of an infectious disease.
Wolfram System Modeler
評価版
ご購入
System ModelerはWindows,macOS,
Linuxで
日本語と英語でご利用になれます »
ご質問やコメントはWolframエキスパートまでお寄せください »