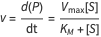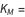Biologie informatique

Modélisez, simulez et visualisez les systèmes biologiques et biochimiques. Modélisez et simulez la cinétique des réactions.

Équation de Michaelis–Menten

En utilisant l’équation de Michaelis–Menten, on peut simplifier une réaction enzymatique simple qui n’est pas affectée par la rétroaction négative, les effets allostériques ou la coopérativité. Ce modèle vise à expliquer pourquoi il en est ainsi. La bibliothèque gratuite BioChem de Modelica est nécessaire pour exécuter cet exemple. Vous pouvez la télécharger ici.

Télécharger le modèle complet

Introduction

L’équation de Michaelis–Menten est l’un des modèles les plus importants pour les interactions enzyme-substrat. Elle est utilisée pour étudier la cinétique d’un large éventail de fonctions biologiques, telles que la réponse immunitaire. Alors qu’un modèle d’action de masse d’une interaction enzyme-substrat passerait par une étape intermédiaire avec un complexe enzyme-substrat, l’équation de Michaelis–Menten suppose que ce complexe entre rapidement dans un état quasi stable et peut être approximé. Il n’est donc pas nécessaire de mesurer le taux de formation de ce complexe, ce qui n’est pas possible dans la pratique.

Le modèle

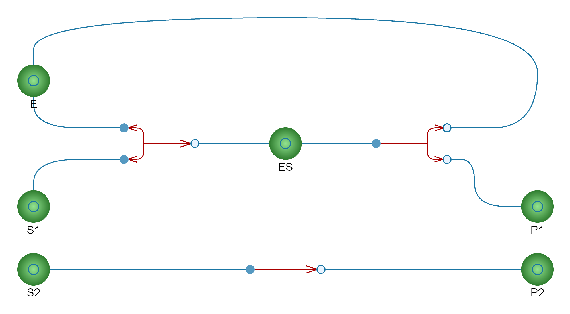
Le modèle d’action de masse comprend quatre substances, alors que le modèle de Michaelis–Menten n’en comprend que deux. Pourtant, dans certaines circonstances, le comportement des deux modèles est presque identique.

Représentation visuelle dans System Modeler

Le modèle a été construit dans System Modeler, ce qui permet d’obtenir une représentation visuelle du modèle.

L’enzyme et le complexe enzyme-substrat sont impliqués dans la description de l’équilibre entre le substrat et le produit à l’aide de la formule de taux de Michaelis–Menten.

où

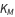incorpore toutes les constantes de taux

La constante de Michaelis est constituée des trois constantes de vitesse de réaction du modèle d’action de masse régulier, formulées pour représenter un flux de réaction net.

est appelée constante de Michaelis, où 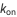, , 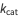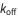sont les constantes de liaison de l’enzyme, de formation du produit et de désolidarisation du substrat, respectivement, comme on le voit ci-dessous.

E+S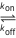

Simulation

Le modèle prend vie

Explorez la façon dont les constantes de vitesse affectent la réaction à l’aide de curseurs dynamiques.

On peut explorer le modèle à l’aide de la fonction Manipulate dans Wolfram Language. Dans le notebook téléchargeable, vous pouvez faire glisser les curseurs et voir comment le système réagit.

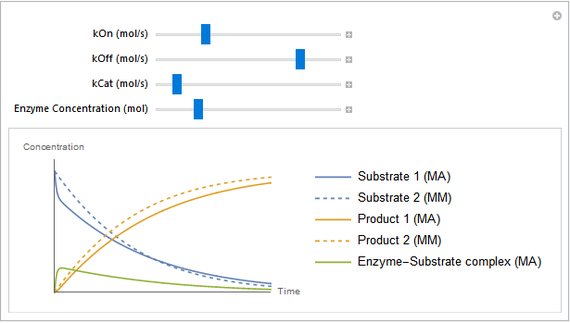
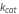La modification en temps réel des valeurs des constantes de vitesse permet d’expérimenter et de mieux comprendre la formule de Michaelis–Menten et ses constantes associées, telles que

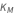Wolfram System Modeler

Essayez Achetez System Modeler est disponible en anglais
et en japonais
sur Windows, macOS et Linux »

Vous avez des questions ou des commentaires ? Contactez un expert Wolfram »

Plus d'apprentissage

Assistance technique

Solutions Wolfram

Solutions Wolfram pour l'éducation

Démarrer

Développez vos compétences

Travaillez avec nous

Programmes pédagogiques pour adultes

Programmes pédagogiques pour les jeunes

Lecture

System Modeler

Biologie informatique

Équation de Michaelis–Menten

Introduction

Le modèle

L’enzyme et le complexe enzyme-substrat sont impliqués dans la description de l’équilibre entre le substrat et le produit à l’aide de la formule de taux de Michaelis–Menten.

où

est appelée constante de Michaelis, où , , sont les constantes de liaison de l’enzyme, de formation du produit et de désolidarisation du substrat, respectivement, comme on le voit ci-dessous.

E+S

Simulation

On peut explorer le modèle à l’aide de la fonction Manipulate dans Wolfram Language. Dans le notebook téléchargeable, vous pouvez faire glisser les curseurs et voir comment le système réagit.

Wolfram System Modeler

Équation de Michaelis–Menten

les dernières versions de System Modeler et Mathematica.

Introduction

Le modèle

L’enzyme et le complexe enzyme-substrat sont impliqués dans la description de l’équilibre entre le substrat et le produit à l’aide de la formule de taux de Michaelis–Menten.

où

est appelée constante de Michaelis, où , , sont les constantes de liaison de l’enzyme, de formation du produit et de désolidarisation du substrat, respectivement, comme on le voit ci-dessous.

E+S

Simulation

On peut explorer le modèle à l’aide de la fonction Manipulate dans Wolfram Language. Dans le notebook téléchargeable, vous pouvez faire glisser les curseurs et voir comment le système réagit.

Wolfram System Modeler