Génie électrique
Utilisez System Modeler pour construire et étudier des circuits électriques, de l’électronique de puissance et des machines électriques. Combinez des composants électriques et mécaniques pour construire des modèles de systèmes complets. Effectuez des tâches d’analyse et mesurez les performances.
Pendule inversé : linéarisation d’un modèle symbolique
Le modèle
Dans cet exemple, un régulateur PID est utilisé pour maintenir le pendule en position verticale. Le point de pivot du pendule est monté sur un chariot qui peut se déplacer horizontalement, contrôlé par un moteur et un système d’engrenages.
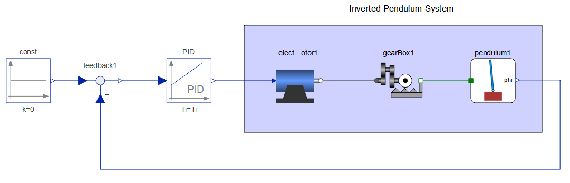
Conception de la commande
Le système du pendule inversé est linéarisé autour de sa position verticale. La longueur du pendule est conservée sous forme symbolique. Le système de commande est ensuite conçu en réglant les paramètres PID pour différentes longueurs du pendule.
Nouveautés de System Modeler 12.0
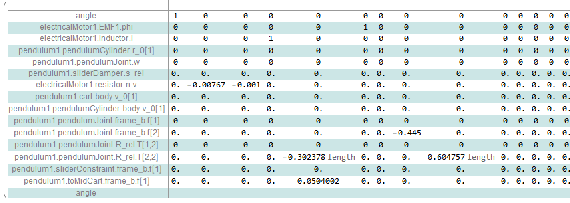
Obtenez une linéarisation symbolique avec les paramètres symboliques sélectionnés.
La stabilité du système combiné composé du régulateur PID et du pendule inversé est vérifiée à l’aide du diagramme de Nyquist. La fonction de transfert en boucle ouverte du système combiné présente un pôle instable et un encerclement autour de {-1,0} dans le sens inverse des aiguilles d’une montre. Comme le pôle instable et l’encerclement s’annulent, on peut en déduire que le système en boucle fermée n’aura pas de pôles instables.
Vérifiez la stabilité
Utilisez le diagramme de Nyquist pour vérifier les pôles instables du système en boucle fermée.

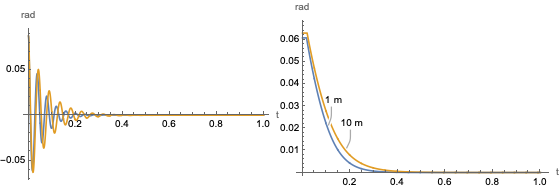
Après avoir vérifié la stabilité, le modèle est simulé. Vous pouvez maintenant observer les données brutes des oscillations et tracer l’enveloppe de la réponse. Vous pouvez voir qu’avec une augmentation de la longueur, le temps nécessaire pour atteindre l’état stable augmente.
Déployez le contrôleur
Observez le comportement du système pour différentes longueurs.
Wolfram System Modeler
Essayez
Achetez
System Modeler est disponible en anglais
et en japonais
sur Windows, macOS et Linux »
Vous avez des questions ou des commentaires ? Contactez un expert Wolfram »