Refroidissement d’un moteur à courant continu à aimant permanent
Les moteurs à courant continu à aimant permanent (DCPM) génèrent de la chaleur résiduelle, comme n’importe quelle autre machine électrique tournante. Il existe différentes méthodes pour refroidir les moteurs électriques et, dans cet exemple, nous utiliserons la bibliothèque standard de Modelica pour étudier l’une de ces méthodes.
Pour exécuter cet exemple, il vous faut
les dernières versions de System Modeler et Mathematica.
Veuillez choisir :
Obtenirun essai gratuit Continuer
le téléchargement
Le modèle
Le circuit de refroidissement comprend la capacité thermique de l’armature, la conductance thermique entre l’armature et le noyau, la capacité thermique du noyau et la conductance thermique entre le noyau et le tuyau de refroidissement.
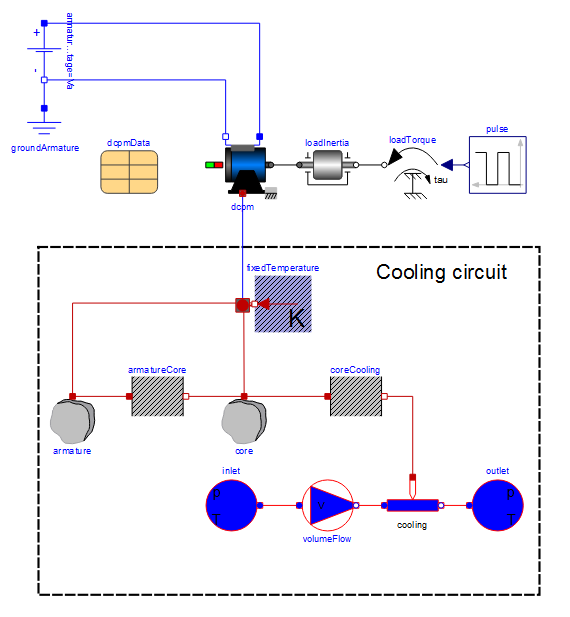
Le schéma montre l’unité de refroidissement en bleu (en bas). Il s’agit d’un circuit d’écoulement de liquide de refroidissement composé d’une entrée, d’un débit volumique de liquide de refroidissement et d’un tuyau relié au noyau et à la sortie.
Résultats de la simulation
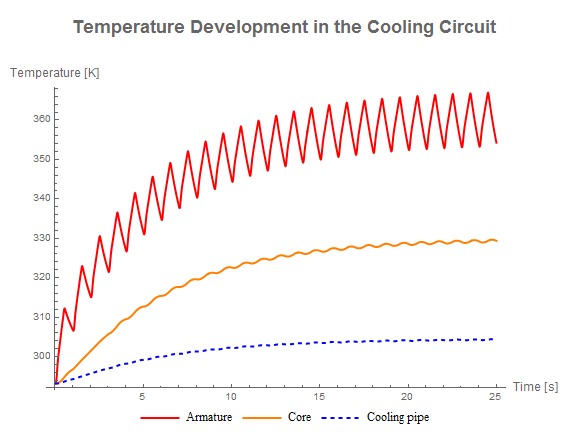
L’évolution de la température dans le circuit de refroidissement. La température baisse à mesure que l’on avance dans le circuit de refroidissement. La température dans le tuyau de refroidissement est la même que la température de sortie.
Il pourrait également être intéressant de voir comment l’évolution de la température change en fonction des différentes propriétés du circuit de refroidissement. Le transfert de chaleur à travers le système est, entre autres, affecté par les capacités de l’armature et du noyau, ainsi que par la conductance entre l’armature et le noyau et entre le noyau et le tuyau de refroidissement.
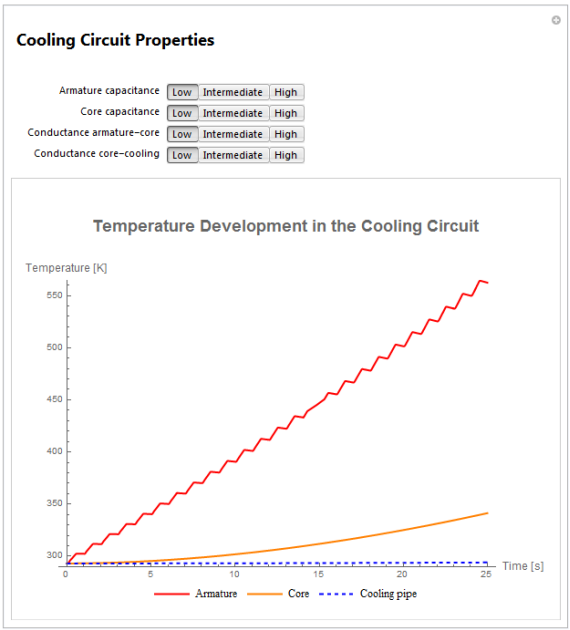
Modifiez les réglages des capacités et des conductances et regardez comment cela affecte l’évolution de la température dans le circuit de refroidissement.
Wolfram System Modeler
Essayez
Achetez
System Modeler est disponible en anglais
et en japonais
sur Windows, macOS et Linux »
Vous avez des questions ou des commentaires ? Contactez un expert Wolfram »