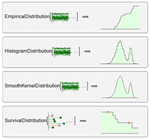
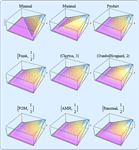
Mathematica 8 introduces fundamentally new ideas in distributional modeling. The first is that of a nonparametric distribution that automates and generalizes a whole range of nonparametric methods used for computing specific distribution properties. The second is that of a derived distribution that is created from any existing distribution through common operations such as functional transformation, truncation, or mixing, etc. The third is that of a distribution defined by a formula such as a PDF, CDF, or survival function. The different types of distributions work together seamlessly, creating a modeling and analysis framework with unprecedented flexibility and ease of use.

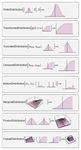
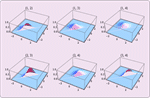
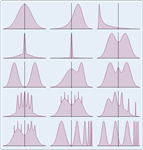
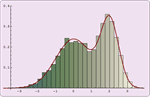
• Nonparametric distributions including empirical, histogram, smooth kernel, etc. »
• Kernel density estimation with automatic fixed or adaptive bandwidth selection. »
• Optimized univariate and multivariate empirical distributions. »
• Nonparametric maximum-likelihood estimation for censored data. »
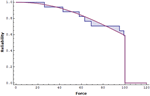
• Efficient survival and reliability modeling with truncated and censored distributions. »
• Derived distributions including transformed, truncated, mixtures, etc. »
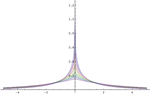
• Univariate and multivariate transformations of random variables. »
• Univariate and joint distributions of order statistics from any distribution. »
• Component mixture distributions with arbitrary component distributions. »
• Parameter mixture distributions with discrete and continuous weight distributions. »
• Truncated distribution of any dimension, continuous and discrete. »
• Censored distribution of any dimension, continuous and discrete. »
• Copula distributions for multiple kernel families and any marginal distributions. »
• Marginal distributions of any dimension from any higher-dimensional distribution. »
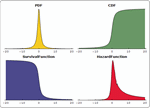
• Distributions defined from formulas of PDF, CDF, or survival functions. »

Create Distributions Directly from Data »	Use Nonparametric Distributions Like Any Other Distribution »	Compute Any of Over 30 Nonparametric Distributional Properties »
Employ Nonparametric Data Models in Any Number of Dimensions »	Estimate Multivariate Nonparametric Probabilities and Expectations »	Analyze Left-, Right-, and Interval-Censored Data »
Use Nonparametric Distributions to Simulate Natural Processes »	Create Confidence Envelopes about Nonparametric Density Estimates »	Solve Optimization Problems in Density Estimation »
Create New Distributions from Existing Ones using Derived Distributions »	Truncate a Distribution »	Perform Affine Transformations on a Normal Distribution »
Apply Censoring to a Distribution »	Create Joint Order Distributions »	Visualize a Marginal Distribution »
Prepare a Table of Special Transformations »	Generate a Gallery of Mixture Distributions »	Use Different Copula Kernels »
Graph of Special Parameter Mixtures »	Simulate a Derived Distribution »	Visualize Iso-Probability Density Levels for a Product Distribution »
Compare Nonparametric and Parametric Reliability Models »	Employ Nonparametric Distributions in Sophisticated Mixture Models »	Create a Hierarchical Parameter Mixture Model »
Study the Properties of a Custom Probability Distribution »	Model Claim Payments for Insurance »	Create Your Own Distribution »

RELATED FUNCTIONS

EmpiricalDistribution  HistogramDistribution  SmoothKernelDistribution  SurvivalDistribution  KernelMixtureDistribution  ProbabilityDistribution  TransformedDistribution  OrderDistribution  MixtureDistribution  ParameterMixtureDistribution  TruncatedDistribution  CensoredDistribution  CopulaDistribution  ProductDistribution  MarginalDistribution