Integer Reversal
Digit-reversal permutation, and in particular bit-reversal permutation, is a reordering technique used in some fast Fourier transform algorithms.
Define a function that generates the reversal permutation of degree 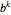 .
.
In[1]:=
reversalperm[k_, b_] := IntegerReverse[Range[0, b^k - 1], b, k] + 1;Generate the bit-reversal permutation for lists of length 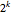 .
.
In[2]:=
Table[reversalperm[k, 2], {k, 0, 5}]Out[2]=
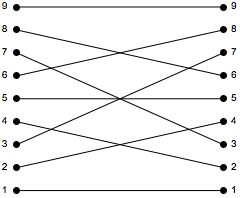
Generate the base-3 digit-reversal permutation for lists of 9 elements.
In[3]:=
reversalperm[2, 3]Out[3]=
Represent those swaps.
In[4]:=
segment[{p1_, p2_}] := {PointSize[Large], Point[{p1, p2}],
Line[{p1, p2}], Text[Last[p1], p1 - {1/2, 0}],
Text[Last[p2], p2 + {1/2, 0}]};In[5]:=

With[{k = 2, b = 3}, Graphics[
segment /@
Thread[{Thread[{0, Range[b^k]}], Thread[{b^k, reversalperm[k, b]}]}]
]]Out[5]=