Representations of Complex Numbers

The new functions ReIm and AbsArg make it easy to convert a complex number to either its Cartesian or polar representation.

Convert a complex number 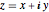to the ordered pair .

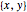In[1]:=

ReIm[3 + 4 I]

Out[1]=

Convert several numbers.

In[2]:=

ReIm[{Pi, -2 I, Sqrt[-I], 3 Exp[I 2 Pi/3]}]

Out[2]=

Convert a complex number 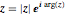to the ordered pair .

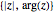In[3]:=

AbsArg[3 + 4 I]

Out[3]=

Convert several numbers.

In[4]:=

AbsArg[{Pi, -2 I, Sqrt[-I], 3 Exp[I 2 Pi/3]}]

Out[4]=

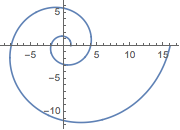
Plot a complex-valued function as a curve in the complex plane.

In[5]:=

ParametricPlot[ReIm[(-2)^x], {x, 0, 4}]

Out[5]=

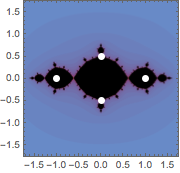
Annotate specific points in a complex-plane plot.

In[6]:=

JuliaSetPlot[-1, PlotRange -> 1.75, Epilog -> {PointSize[Large], White, Point[ReIm[{I/2, -I/2, 1, -1}]]}]

Out[6]=