メルセンヌ(Mersenne)素数と完全数

メルセンヌ素数は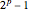の形の素数である．その指数 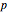自身も素数である．メルセンヌ素数はそれぞれ偶数の完全数に対応する．

メルセンヌ素数の指数のリストを生成する．

In[1]:=

mpe = Table[MersennePrimeExponent[n], {n, 1, 10}]

Out[1]=

対応するメルセンヌ素数を構築する．

In[2]:=

mp = 2^mpe - 1

Out[2]=

対応する完全数を構築する．

In[3]:=

pn = 2^(mpe - 1) (2^mpe - 1)

Out[3]=

In[4]:=

AllTrue[pn, PerfectNumberQ]

Out[4]=

小さいメルセンヌ素数の指数の分布が非常に疎であることを見るために，最初の225個の素数のリストでそれらを赤で強調する．

In[5]:=

primes = Replace[Prime@Range[225], x_?MersennePrimeExponentQ :> Style[x, Red, Bold], 1];

In[6]:=

Multicolumn[primes, Alignment -> {Center, Center}, Spacings -> {1, 1}, Frame -> All, FrameStyle -> Directive[Orange, Dashing[Small]]]

Out[6]=