Encuentre las funciones simbólicas propias de un laplaciano en 1D

Especifique un operador laplaciano en 1D.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}];

Especifique las condiciones de límite homogéneas de Dirichlet para las funciones propias.

In[2]:=

\[ScriptCapitalB]1 = DirichletCondition[u[x] == 0, True];

Encuentre los cinco valores propios y funciones propias.

In[3]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]1}, u[x], {x, 0, \[Pi]}, 5];

Inspeccione los valores propios.

In[4]:=

vals

Out[4]=

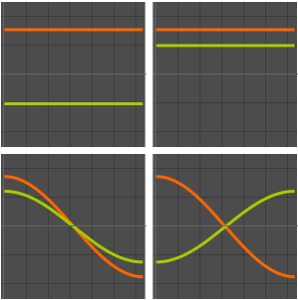
Inspeccione las funciones propias.

In[5]:=

funs

Out[5]=

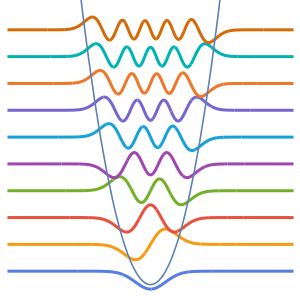
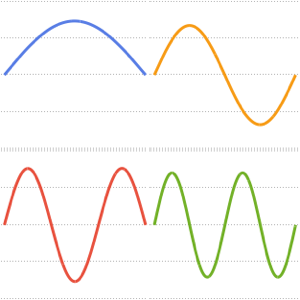
Visualice las funciones propias.

In[6]:=

Plot[Evaluate[funs + 2 Range[5]], {x, 0, \[Pi]}]

Out[6]=

Especifique una condición de límite homogénea de Neumann.

In[7]:=

\[ScriptCapitalB]2 = NeumannValue[0, True];

Encuentre los cinco valores propios y funciones propias más pequeños.

In[8]:=

{vals, funs} = DEigensystem[\[ScriptCapitalL] + \[ScriptCapitalB]2, u[x], {x, 0, \[Pi]}, 5];

Inspeccione los valores propios. Se ha añadido un modo cero en relación con las condiciones de Dirichlet.

In[9]:=

vals

Out[9]=

Los senos han reemplazado a los cosenos en las funciones propias.

In[10]:=

funs

Out[10]=

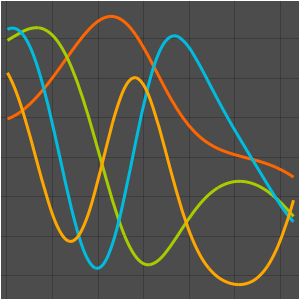
Visualice las funciones propias.

In[11]:=

Plot[Evaluate[funs + 2 Range[5]], {x, 0, \[Pi]}]

Out[11]=