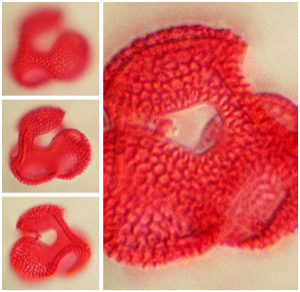
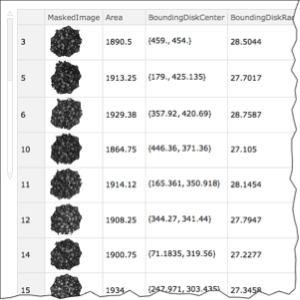
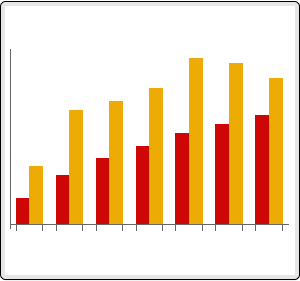
Multi-view Reconstruction

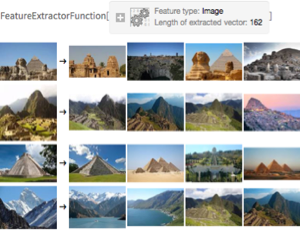
A 3D object can be reconstructed from multiple 2D views. ImageDisplacements is used to determine the parallax from one view to the next. The larger the parallax shift, the closer the object behind the corresponding pixel. With this depth information, you can extrude the vertices of an object mesh obtained through ImageMesh and TriangulateMesh. The result is displayed via texture mapping on the 3D mesh object.

In[1]:=

Obtain an object mask of the central image.

In[2]:=

mask = Erosion[Binarize[imgs[[2]], 0], 1];

Determine the parallax in the left and right images with respect to the center image.

In[3]:=

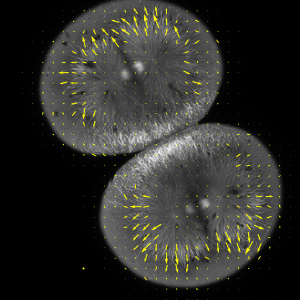
parallaxL = First@ImageDisplacements[imgs[[{2, 1}]]];

In[4]:=

parallaxR = First@ImageDisplacements[imgs[[{2, 3}]]];

Combine these displacements in a total parallax.

In[5]:=

parallax = parallaxL - parallaxR;

In the given setting, the component of the parallax is roughly proportional to the depth of the respective pixel source.

In[6]:=

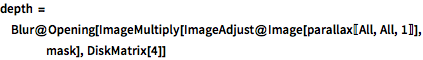
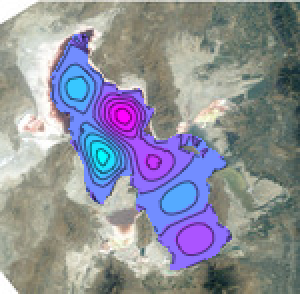
depth = Blur@ Opening[ImageMultiply[ImageAdjust@Image[parallax[[All, All, 1]]], mask], DiskMatrix[4]]

Out[6]=

Construct a depth function.

In[7]:=

depthFunction = ListInterpolation[Transpose@Reverse@ImageData[depth]];

Obtain an object mesh with a refinement that depends on the object's saliency.

In[8]:=

resolution = ImageAdjust@ImageSaliencyFilter[imgs[[2]]];

In[9]:=

resolutionFunction = ListInterpolation[Transpose@Reverse@ImageData@resolution];

In[10]:=

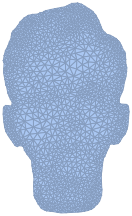
\[CapitalOmega] = TriangulateMesh[ ImageMesh[Erosion[mask, DiskMatrix[2]]], MeshRefinementFunction -> Function[{vertices, area}, area > 32 + 512 (1 - resolutionFunction @@ Mean[vertices])^6] ]

Out[10]=

Extrude the object mesh with the depth function.

In[11]:=

Graphics3D[ GraphicsComplex[ Apply[{##, depthFunction[##]} &, MeshCoordinates[\[CapitalOmega]], {1}], {EdgeForm[], MeshCells[\[CapitalOmega], 2]} ], PlotRange -> Append[Thread[{0, ImageDimensions[mask]}], {0, 1}], BoxRatios -> {1, 1, 2/3}, ViewPoint -> Top ]

Out[11]=

Extract the object texture from the central image.

In[12]:=

texture = SetAlphaChannel[imgs[[2]], mask]

Out[12]=

Map the texture onto the 3D object.

In[13]:=

Graphics3D[ {Texture[texture], GraphicsComplex[ Apply[{##, depthFunction[##]} &, MeshCoordinates[\[CapitalOmega]], {1}], {EdgeForm[], MeshCells[\[CapitalOmega], 2]}, VertexTextureCoordinates -> Map[#/ImageDimensions[texture] &, MeshCoordinates[\[CapitalOmega]]] ] }, PlotRange -> Append[Thread[{0, ImageDimensions[mask]}], {0, 1}], BoxRatios -> {1, 1, 2/3}, Lighting -> {{"Ambient", White}}, ViewPoint -> Top, Boxed -> False ]

Play Animation

Stop Animation