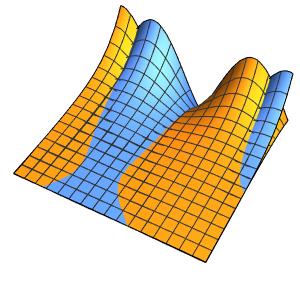
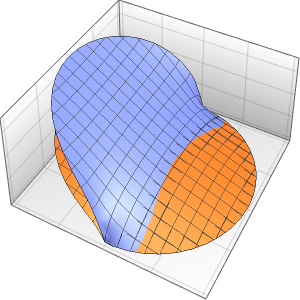
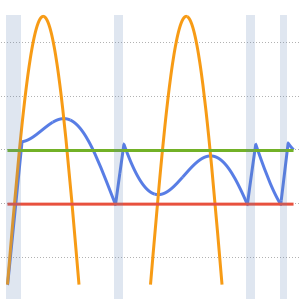
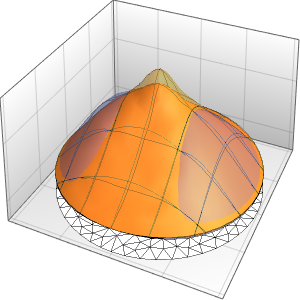
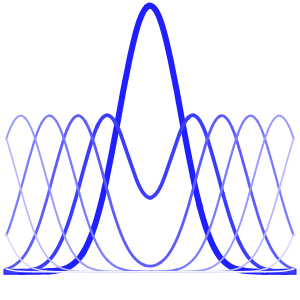
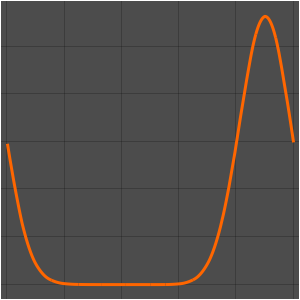
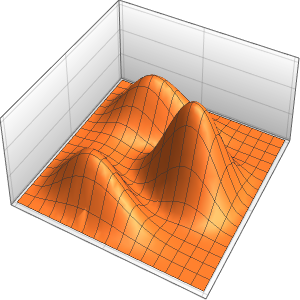
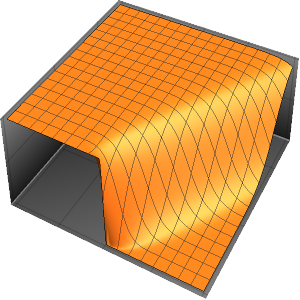
周期境界条件でポアソン方程式を解く

曲面の境界上において周期境界条件でポアソン方程式を解く．

領域を指定する．

In[1]:=

\[CapitalOmega] = RegionDifference[RegionUnion[Disk[], Rectangle[{0, -1}, {2, 1}]], Disk[{2, 0}]];

左辺からの解が領域の右辺にマップされる周期境界条件で，偏微分方程式を解く．

In[2]:=

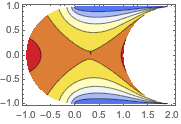
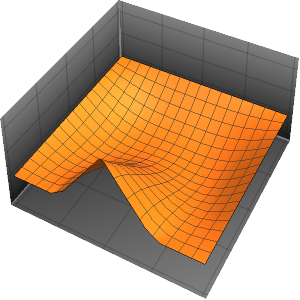
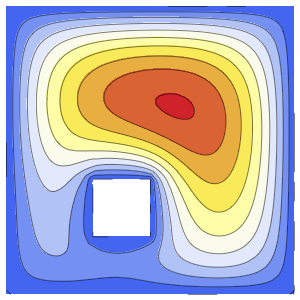
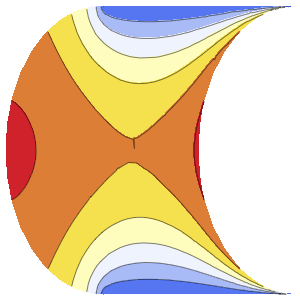
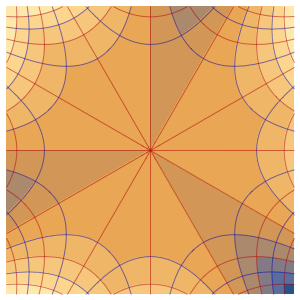
ufun = NDSolveValue[{-\!\( \*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(u[x, y]\)\) == 1, PeriodicBoundaryCondition[u[x, y], (x - 2)^2 + y^2 == 1, Function[x, x - {2, 0}]], DirichletCondition[ u[x, y] == 0, (0 <= x <= 2 && (y <= -1 || y >= 1))]}, u, {x, y} \[Element] \[CapitalOmega]];

解を可視化する．

In[3]:=

ContourPlot[ufun[x, y], {x, y} \[Element] \[CapitalOmega], ColorFunction -> "TemperatureMap", AspectRatio -> Automatic] // Quiet

Out[3]=