Solve an Initial-Boundary Value Problem for a First-Order PDE

Specify a linear first-order partial differential equation.

In[1]:=

eqn = D[u[t, x], t] + D[u[t, x], x] == 0;

Prescribe initial and boundary conditions for the equation.

In[2]:=

ibc = {u[t, 0] == 0, u[0, x] == E^(-x) Sin[x]^2};

Solve the problem using DSolveValue.

In[3]:=

sol = DSolveValue[{eqn, ibc}, u[t, x], {t, x}] // FullSimplify

Out[3]=

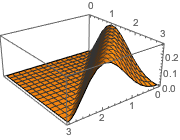
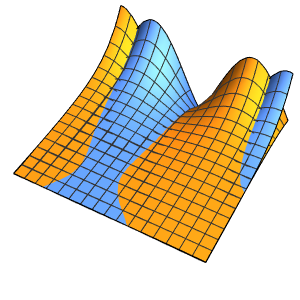
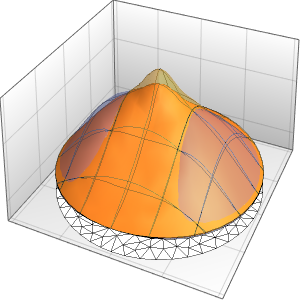
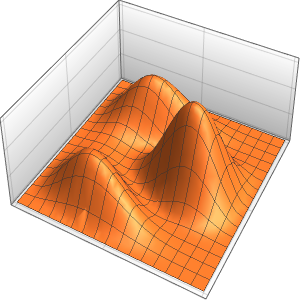
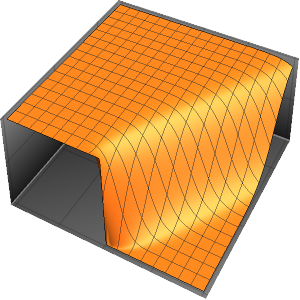
Visualize the solution.

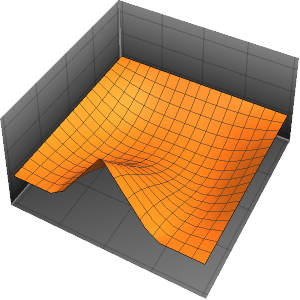
In[4]:=

Plot3D[sol // Evaluate, {t, 0, 3}, {x, 0, 3}, Exclusions -> None]

Out[4]=