Model the Flow of Heat in an Insulated Bar

Model the flow of heat in a bar of length 1 that is insulated at both ends.

In[1]:=

heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];

Specify that no heat flows through the ends of the bar.

In[2]:=

bc = {Derivative[1, 0][u][0, t] == 0, Derivative[1, 0][u][1, t] == 0};

Specify an initial condition.

In[3]:=

ic = u[x, 0] == 20 + 80 x;

Solve the heat equation subject to these conditions.

In[4]:=

sol = DSolve[{heqn, bc, ic}, u[x, t], {x, t}]

Out[4]=

Extract a few terms from the Inactive sum.

In[5]:=

approxsol = u[x, t] /. sol[[1]] /. {Infinity -> 4} // Activate // Expand

Out[5]=

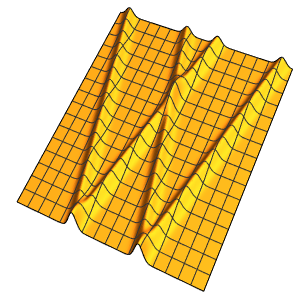
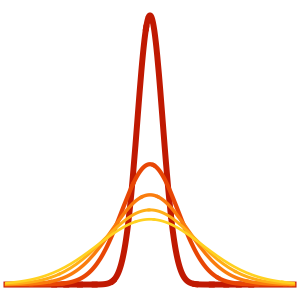
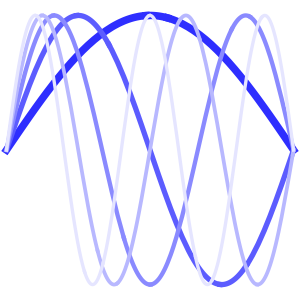
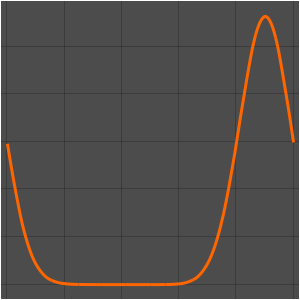
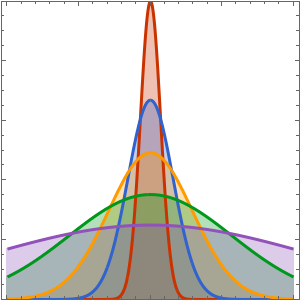
Visualize the evolution of the temperature to the steady-state value of 60°.

In[6]:=

Plot[Table[approxsol, {t, 0.02, 0.9, 0.07}] // Evaluate, {x, 0, 1}, AxesOrigin -> {0, 0}, PlotRange -> All]

Out[6]=