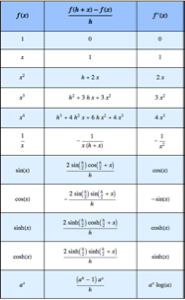
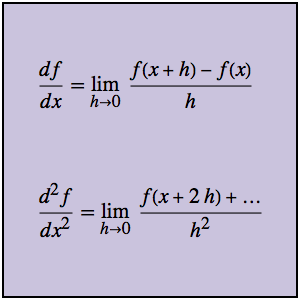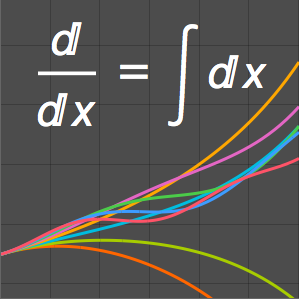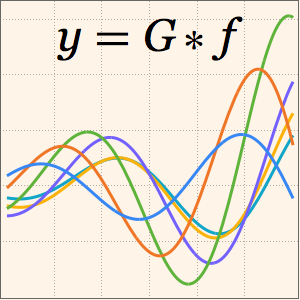Lösen Sie ein Randwertproblem mithilfe einer Greenschen Funktion

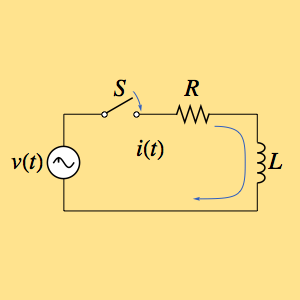
Lösen Sie die folgende Differentialgleichung zweiter Ordnung mit vorgegebenen homogenen Randbedingungen.

In[1]:=

eqn = -u''[x] - u'[x] + 6 u[x] == f[x];

In[2]:=

bc0 = u[0] == 0;

In[3]:=

bc1 = u[1] == 0;

Der Impulsterm ist durch die folgende Funktion f[x] gegeben.

In[4]:=

f[x_] := E^(-a x)

Berechnen Sie die Greensche Funktion für den entsprechenden Differentialoperator.

In[5]:=

gf[y_, x_] = GreenFunction[{eqn[[1]], bc0, bc1}, u[x], {x, 0, 1}, y]

Out[5]=

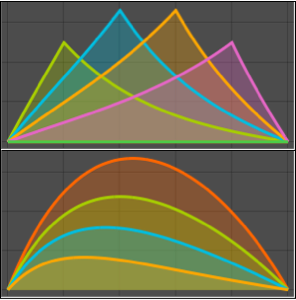
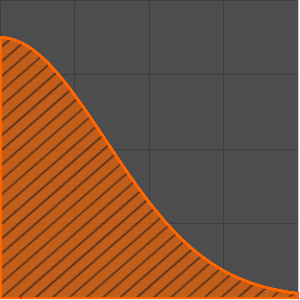
Plotten Sie die Greensche Funktion für verschiedene zwischen 0 und 1 liegende Werte von .

In[6]:=

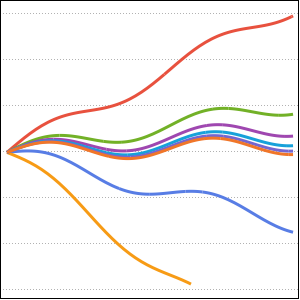
Plot[Table[gf[y, x], {y, 0, 1, 0.2}] // Evaluate, {x, 0, 1}]

Out[6]=

Die Lösung der ursprünglichen Differentialgleichung mit dem gegebenen Impulsterm kann nun mit einem Faltungsintegral auf dem Intervall berechnet werden.

In[7]:=

sol = Integrate[gf[y, x] f[y], {y, 0, 1}, Assumptions -> 0 < x < 1] // Simplify

Out[7]=

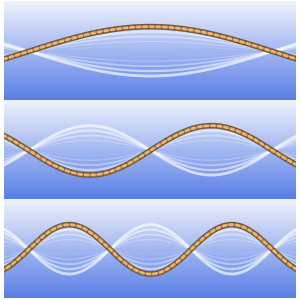
Plotten Sie die Lösung für verschiedene Werte des Parameters .

In[8]:=

Plot[Table[sol, {a, {1/4, 1, 2, 4}}] // Evaluate, {x, 0, 1}]

Out[8]=