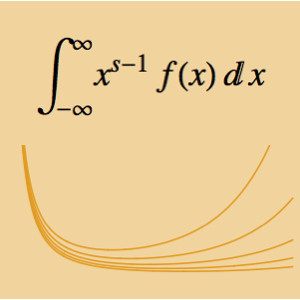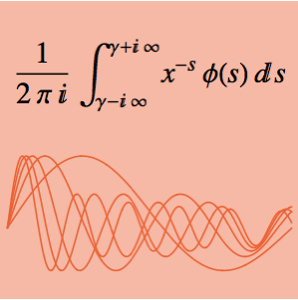Lösen Sie eine Volterra-Integralgleichung
Lösen Sie mit DSolveValue eine Volterra-Integralgleichung.
In[1]:=
eqn = y[x] == x^3 + \[Lambda] \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(x\)]\(\((t - \ x)\) y[
t] \[DifferentialD]t\)\);In[2]:=
sol = DSolveValue[eqn, y[x], x]Out[2]=

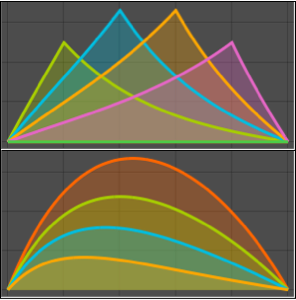
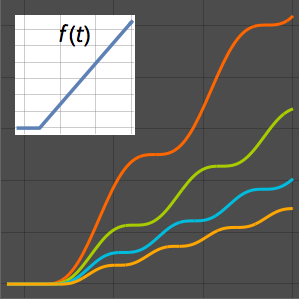
Plotten Sie die Lösung für unterschiedliche λ-Werte.
In[3]:=
Plot[Table[sol, {\[Lambda], 1, 3, 0.5}] // Evaluate, {x, 0, 20}]Out[3]=

Lösen Sie eine schwach singuläre Volterra-Integralgleichung.
In[4]:=
eqn = y[x] == x^a - \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(x\)]\(
\*FractionBox[\(y[t]\),
SqrtBox[\(x - t\)]] \[DifferentialD]t\)\);Finden Sie mit DSolveValue einen Ausdruck für die Lösung.
In[5]:=
sol = DSolveValue[eqn, y[x], x]Out[5]=
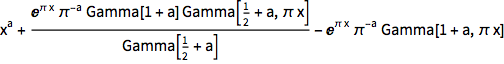
Plotten Sie die Lösung.
In[6]:=
Plot[Table[sol, {a, 1, 4, 0.7}] // Evaluate, {x, 0, 2}]Out[6]=