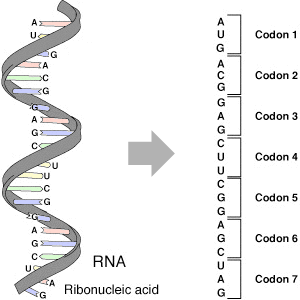
Zipf's Law

Zipf's law states that in a corpus of a language, the frequency of a word is inversely proportional to its rank in the global list of words after sorting by decreasing frequency. This example demonstrates the law with the set of words in Miguel de Cervantes's novel Don Quixote, using the new functions WordCount and WordCounts.

ExampleData contains the text in Spanish of the first volume of Don Quixote.

In[1]:=

textSpanish = ExampleData[{"Text", "DonQuixoteISpanish"}];

The sample considered here is comprised of more than 180,000 words.

In[2]:=

WordCount[textSpanish]

Out[2]=

The counts of each distinct word are given as an association by WordCounts. The result is already sorted by decreasing counts.

In[3]:=

association = WordCounts[textSpanish];

In[4]:=

Take[association, 10]

Out[4]=

Take the counts of the first 1,000 most frequent words.

In[5]:=

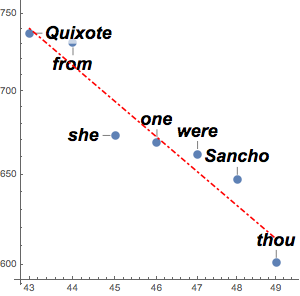
counts = Take[Values@association, 1000];

To approximate those counts with a power law, take logarithms to use linear fitting. Zipf's law asserts that the exponent should be approximately 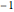, and the result is a close value.

In[6]:=

f[x_] = Fit[Log[Transpose[{Range[1000], counts}]], {1, x}, x]

Out[6]=

Visualize the fit together with the actual data.

In[7]:=

Show[ ListLogLogPlot[counts, PlotStyle -> PointSize[0.02]], LogLogPlot[Exp[f[Log[x]]], {x, 1, 1000}, PlotStyle -> Directive[DotDashed, Red]], AspectRatio -> 1, PlotRange -> All ]

Out[7]=

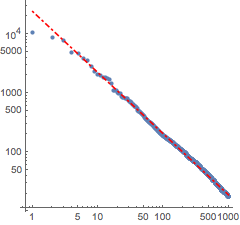
Zipf's law holds in any language, so the same computation is performed with the English version of Don Quixote.

In[8]:=

textEnglish = ExampleData[{"Text", "DonQuixoteIEnglish"}];

In[9]:=

associationEnglish = WordCounts[textEnglish]; countsEnglish = Take[Values@associationEnglish, 1000];

In[10]:=

Take[associationEnglish, 10]

Out[10]=

Again, the exponent found is close to .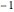

In[11]:=

Fit[Log[Transpose[{Range[1000], countsEnglish}]], {1, x}, x]

Out[11]=