Analytic Center

A convex polygon can be represented as intersections of half-planes . The analytic center can be defined as a point inside the polygon that maximizes the product of distances to the sides. The distance of a point in the polyhedron to each side is 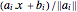, and so the analytic center is , which maximizes .

This example demonstrates how exponential cone constraints may be used with ConicOptimization to find the analytic center, as well as how the inequality representation for a polygon may be extracted using LinearOptimization.

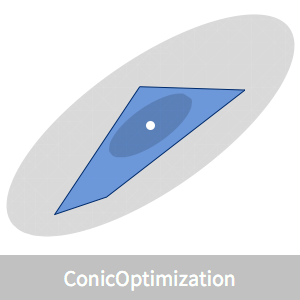
Take a convex polygon.

Extract the coefficients for each side.

The scalar inequalities corresponding to the polygon are:

To express the problem as a convex minimization, take and negate the objective . The transformed objective is .

Because a sum of logarithms is concave, the negation is convex, and so an auxiliary variable can be introduced as the objective function with subject to the constraint .

Visualize the location of the analytic center.

There are simple formulas that give the inscribed and covering ellipsoids that are centered at the analytic center.