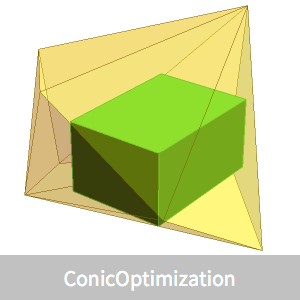
Maximum-Volume Cuboid
Find the maximum-volume axis-parallel cuboid inscribed in a convex polyhedron 
.
This example demonstrates how optimization of a product of positive terms can be expressed in terms of power-cone constraints that can be used with ConicOptimization to find the optimum.
Consider a random convex polyhedron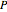 
constructed as the convex hull of random points.
For the cuboid, find a lower-corner point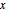 
and a vector of side length 
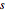so that the cuboid is represented in the Wolfram Language by 
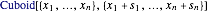. The volume of the cuboid is just the product of the side lengths, so the objective is to maximize 
. If all of the corners of the cuboid are in 
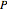, then all of the points in the cuboid are also. The corners may be described by 
, where 
is in the set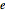 
of all possible n‐tuples of elements from 
.
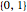The problem becomes:
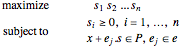
Since 
is non-negative, maximizing the product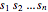 
is the same as maximizing the geometric mean 
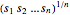, which is known to be concave. Maximizing 
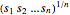is equivalent to minimizing 
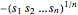, which is convex. Using an auxiliary variable 
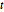, reformulate the problem with a linear objective function -
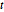with the additional constraints 
.
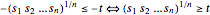The problem becomes:
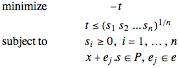
The power cone is the set of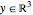 
such that 
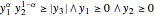, and may be expressed in the Wolfram Language by 
.
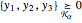Since 
, the new constraint 
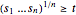can be satisfied for non-negative 
and is equivalent to 
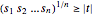. This can be written as a series of power cone constraints
For 
the problem becomes:
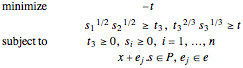
A convex polyhedron can be represented as intersections of half-spaces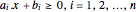 
. Extract the coefficients 
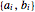for each side.
Solve the problem.
Show the maximum-volume-inscribed cuboid.
Instead of a polyhedron, take any convex conic representable set K⊆n—for example, an ellipsoid. A vertex of the cuboid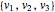 
is inside the ellipsoid iff 
.
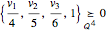Solve the problem.
Plot the result.
