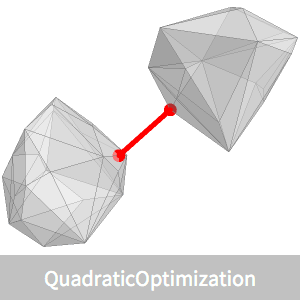
Minimal Bounding Ellipsoid

Given a set of 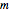points in dimensions, find the Löwner–John ellipsoid that is the smallest-volume ellipsoid enclosing all of the points.

This example demonstrates that for problems expressed in terms of highly nonlinear convex objective functions and constraints, NMinimize can do transformations that make the problem easily solved by convex optimization.

An ellipsoid in can be described by the set of points 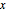such that , where 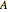is a positive semidefinite 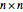matrix and 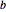is an -vector. The volume of the ellipsoid is proportional to 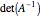. 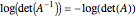is convex so finding the solution of

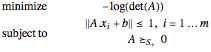
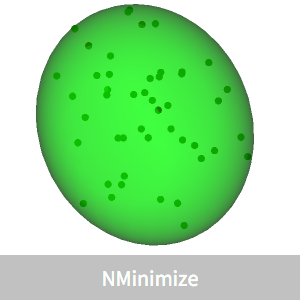
The example shown here is done for a random set of points in three dimensions so that it can be visualized, but the solution algorithm can handle larger dimensions .

Find the solution using NMinimize.

In three dimensions, the ellipsoid can be described in terms of the Ellipsoid graphics primitive.

BoundingRegion can find an enclosing ellipsoid faster, but it has greater volume.