Verborgene Zustände ermitteln, die bestimmten Emissionen von HMM-Prozessen zugrundeliegen
Bei einem gegebenen HMM und einer beobachteten Sequenz ist es im Allgemeinen unmöglich, die entsprechende Sequenz unbeobachteter Zustände des Systems eindeutig wiederherzustellen. Mathematica 10 unterstützt zwei häufig genutzte Kriterien zum Ermitteln der "optimalen" Zustandssequenz in Bezug auf die gegebenen Beobachtungen: den Viterbi-Algorithmus und die Posterior-Dekodierung. Die mit Viterbi dekodierte Sequenz maximiert die Verbundwahrscheinlichkeit der Sequenz der verborgenen Zustände und Emissionen. Die Posterior-dekodierte Sequenz maximiert die Aufenthaltswahrscheinlichkeit jeder einzelnen Emission im verborgenen Zustand.
Generieren Sie ein HMM mit Links-Rechts-Topologie und überlappenden Emissionsverteilungen.
| Out[2]= | 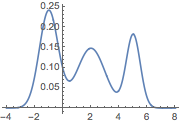 |
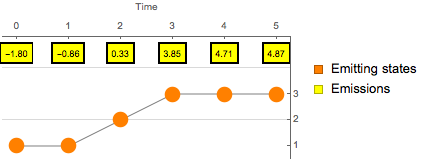
Bestimmen Sie die wahrscheinlichste Sequenz von verborgenen Zuständen mithilfe des Viterbi-Algorithmus.
| Out[4]= | 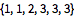 |
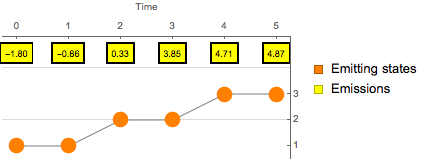
Bestimmen Sie die Sequenz der jeweils wahrscheinlichsten verborgenen Zustände mithilfe der Posterior-Dekodierung.
| Out[5]= | 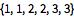 |
Ebenso lassen sich multivariate Emissionen dekodieren.
| Out[7]= |  |
Ermitteln Sie die wahrscheinlichste Zustandssequenz mithilfe des Viterbi-Algorithmus.
| Out[9]= | 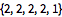 |
Ermitteln Sie die Sequenz der jeweils wahrscheinlichsten Zustände mithilfe der Posterior-Dekodierung.
| Out[10]= | 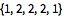 |