Verborgene Markov-Prozesse mit Nullzuständen 

Bei verborgenen Markov-Prozessen mit Zuständen, die keine Symbole ausgeben, wird oft die Topologie von verborgenen Zuständen angewendet, d.h. die Übergangsmatrix ist dünn besetzt. Dies ermögicht Übergänge zwischen emittierenden Zuständen, die unter der gewählten Topologie nicht möglich wären. Dank der strukturierten Übergangsmatrix lassen sich HMMs mit Nullzuständen oft einfacher schätzen als ihre dichten Gegenstücke.

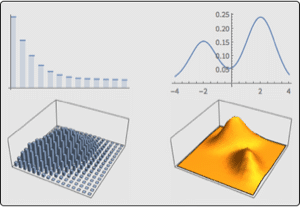
Bestimmen Sie die Aufenthaltswahrscheinlichkeit des Sytems in einem von sechs möglichen nicht beobachtbaren Zuständen. Berechnen Sie außerdem die Matrix der bedingten Übergangswahrscheinlichkeiten ziwschen diesen Zuständen.

In[1]:=

X Subscript[p, 0] = {1/2, 1/3, 0, 0, 1/12, 1/12}; \[ScriptCapitalP] = SparseArray[{ {1, 2} -> 0.85, {1, 3} -> 0.15, {2, 3} -> 0.5, {2, 4} -> 0.5, {3, 5} -> 0.65, {3, 4} -> 0.22, {3, 6} -> 0.13, {4, 1} -> 0.25, {4, 3} -> 0.08, {4, 5} -> 0.67, {5, 2} -> 0.3, {5, 6} -> 0.7, {6, 4} -> 0.6, {6, 5} -> 0.4}];

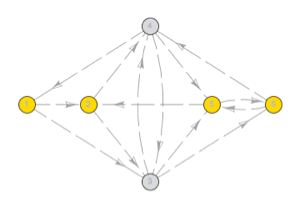
Visualisieren Sie die Topologie der Übergänge zwischen verborgenen Zuständen.

In[2]:=

X gr = Graph[DiscreteMarkovProcess[Subscript[p, 0], \[ScriptCapitalP]], ImageSize -> 300, GraphLayout -> {"MultipartiteEmbedding", "VertexPartition" -> {1, 1, 2, 1, 1}}]

Out[2]=

Bestimmen Sie die Häufigkeit, mit der das System ein kategoriales Signal pro unbeobachtbaren Zustand aussendet. Die Emissionen sind von 1 bis 6 durchnummeriert. Es treten keine Emissionen auf, wenn das System sich entweder in Zustand 3 oder Zustand 4 befindet – also in Nullzuständen.

In[3]:=

X em = {{1/2, 1/4, 1/8, 1/16, 1/32, 1/32}, {1/32, 1/2, 1/4, 1/8, 1/16, 1/32}, None, None, {1/8, 1/16, 1/32, 1/32, 1/2, 1/4}, {1/4, 1/8, 1/16, 1/32, 1/ 32, 1/2}};

Definieren Sie einen verborgenen Markov-Prozess, der beobachtbare Emissionen beschreibt.

In[4]:=

X hmm = HiddenMarkovProcess[Subscript[p, 0], \[ScriptCapitalP], em];

Simulieren Sie eine Emissionensequenz.

In[5]:=

X emissions = RandomFunction[hmm, {0, 15}]

Out[5]=

Ermitteln Sie die wahrscheinlichste Sequenz der dem System zugrundeliegenden unbeobachtbaren Zustände.

In[6]:=

X likelyPath = FindHiddenMarkovStates[emissions, hmm]

Out[6]=

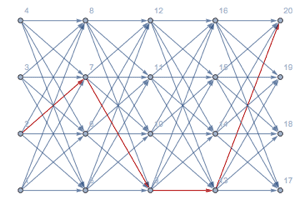
Beachten Sie, dass die dekodierte Sequenz der Zustände aufgrund des Auftretens von Nullzuständen länger ist als die Sequenz der Emissionen. Visualisieren Sie die Sequenz der dekodierten verborgenen Zustände.

In[7]:=

X verticesVisited = likelyPath["Values"]; edgesTraversed = DirectedEdge @@@ Partition[verticesVisited, 2, 1];

Ermitteln Sie den verborgenen Markov-Prozess ohne verborgene Zustände, der allen Emissionssequenzen dieselben Wahrscheinlichkeiten zuordnet.

In[8]:=

X hmmReduced = HiddenMarkovProcess[hmm]

Out[8]=

Bilden Sie kurze Sequenzen von Emissionen und vergewissern Sie sich, dass ihnen von beiden Prozessen die gleiche Likelihood zugeordnet wird.

In[9]:=

X shortEmissions = Join[Tuples[Range[6], 1], Tuples[Range[6], 2], Tuples[Range[6], 3]];

In[10]:=

X llOriginal = Likelihood[hmm, #] & /@ shortEmissions;

In[11]:=

X llReduced = Likelihood[hmmReduced, #] & /@ shortEmissions;

In[12]:=

X llOriginal == llReduced

Out[12]=

Erzeugen Sie ein Ensemble aus längeren Emissionssequenzen und verwenden Sie diese zum Schätzen der Parameter des verborgenen Markov-Prozesses mit Nullzuständen.

In[13]:=

X longEmissions = RandomFunction[hmm, {0, 100}, 100];

In[14]:=

X esthmm = EstimatedProcess[longEmissions, HiddenMarkovProcess[6, 6], hmm]

Out[14]=

Vergleichen Sie die Log-Likelihoods der Emissionen.

In[15]:=

X LogLikelihood[esthmm, longEmissions]

Out[15]=

In[16]:=

X LogLikelihood[hmm, longEmissions]

Out[16]=