Processos ocultos de Markov com estados silenciosos 

Processos ocultos de Markov com estados silenciosos são normalmente usados com topologia rígida de dinâmica de estados ocultos, isto é, a matriz de transição é esparsa, para permitir transições entre estados emissores que são impossíveis sob a topologia escolhida. Graças à estruturada matriz de transição, modelos ocultos de Markov com estados silenciosos são frequentemente mais fáceis de estimar que seus análogos densos.

Defina as probabilidades iniciais do sistema estando em um dos seis possíveis estados inobserváveis, assim como a matriz das probabilidades de transição condicional entre esses estados.

In[1]:=

X Subscript[p, 0] = {1/2, 1/3, 0, 0, 1/12, 1/12}; \[ScriptCapitalP] = SparseArray[{ {1, 2} -> 0.85, {1, 3} -> 0.15, {2, 3} -> 0.5, {2, 4} -> 0.5, {3, 5} -> 0.65, {3, 4} -> 0.22, {3, 6} -> 0.13, {4, 1} -> 0.25, {4, 3} -> 0.08, {4, 5} -> 0.67, {5, 2} -> 0.3, {5, 6} -> 0.7, {6, 4} -> 0.6, {6, 5} -> 0.4}];

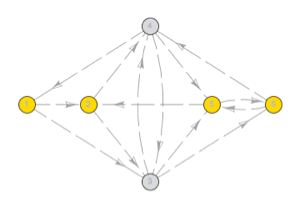
Visualize a topologia de transições entre estados ocultos.

In[2]:=

X gr = Graph[DiscreteMarkovProcess[Subscript[p, 0], \[ScriptCapitalP]], ImageSize -> 300, GraphLayout -> {"MultipartiteEmbedding", "VertexPartition" -> {1, 1, 2, 1, 1}}]

Out[2]=

Defina frequências do sistema emitindo um sinal categórico para cada estado inobservável. Emissões são classificadas de 1 até 6. Nenhuma emissão é realizada quando o sistema se acha tanto no estado 3 quanto no estado 4; ou seja, esses estados são silenciosos.

In[3]:=

X em = {{1/2, 1/4, 1/8, 1/16, 1/32, 1/32}, {1/32, 1/2, 1/4, 1/8, 1/16, 1/32}, None, None, {1/8, 1/16, 1/32, 1/32, 1/2, 1/4}, {1/4, 1/8, 1/16, 1/32, 1/ 32, 1/2}};

Defina processos ocultos de Markov que descrevam emissões inobserváveis.

In[4]:=

X hmm = HiddenMarkovProcess[Subscript[p, 0], \[ScriptCapitalP], em];

Simule uma sequência de emissões.

In[5]:=

X emissions = RandomFunction[hmm, {0, 15}]

Out[5]=

Ache a sequência mais provável dos estados inobserváveis subjacentes ao sistema.

In[6]:=

X likelyPath = FindHiddenMarkovStates[emissions, hmm]

Out[6]=

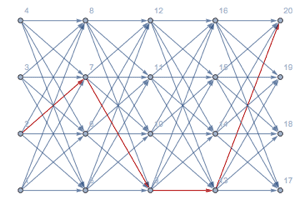
Note que a sequência decodificada de estados é mais longa que a sequência de emissões, devido à presença de estados silenciosos. Visualize a sequência de estados silenciosos decodificados.

In[7]:=

X verticesVisited = likelyPath["Values"]; edgesTraversed = DirectedEdge @@@ Partition[verticesVisited, 2, 1];

Encontre o processo oculto de Markov sem estados ocultos que atribui as mesmas probabilidades para todas as sequências de emissões.

In[8]:=

X hmmReduced = HiddenMarkovProcess[hmm]

Out[8]=

Construa curtas sequências de emissões e confirme que ambos os processos atribuem-lhes probabilidades iguais.

In[9]:=

X shortEmissions = Join[Tuples[Range[6], 1], Tuples[Range[6], 2], Tuples[Range[6], 3]];

In[10]:=

X llOriginal = Likelihood[hmm, #] & /@ shortEmissions;

In[11]:=

X llReduced = Likelihood[hmmReduced, #] & /@ shortEmissions;

In[12]:=

X llOriginal == llReduced

Out[12]=

Gere um conjunto de sequências de emissões mais longas e utilize-as para estimar os parâmetros do processo oculto de Markov com estados silenciosos.

In[13]:=

X longEmissions = RandomFunction[hmm, {0, 100}, 100];

In[14]:=

X esthmm = EstimatedProcess[longEmissions, HiddenMarkovProcess[6, 6], hmm]

Out[14]=

Compare as verossimilhanças logarítmicas das emissões.

In[15]:=

X LogLikelihood[esthmm, longEmissions]

Out[15]=

In[16]:=

X LogLikelihood[hmm, longEmissions]

Out[16]=