Efectúe corrección de errores tipográficos sin un diccionario
Modelar la secuencia de caracteres escritos como observaciones y la secuencia de caracteres escritos correctos como estados ocultos, este ejemplo utiliza dos modelos diferentes para la evolución de caracteres correctos para corregir errores tipográficos. El primer modelo utiliza el proceso de Markov de primer orden para codificar frecuencias de lo que sigue al carácter dado. El segundo modelo utiliza estados de Markov de segundo orden para codificar frecuencias de lo que sigue a los últimos dos caracteres dados.
Tome El origen de las especies de Darwin y convierta todos los símbolos que no son letras en espacios.
| In[1]:= |  X |
| In[2]:= | X |
Introduzca errores tipográficos, a una tasa del 20%, al remplazar al azar un carácter con uno de sus vecinos inmediatos en un teclado estándar QWERTY. El carácter de espacio nunca es mal escrito.
| In[4]:= |  X |
| In[5]:= |  X |
| Out[6]= | 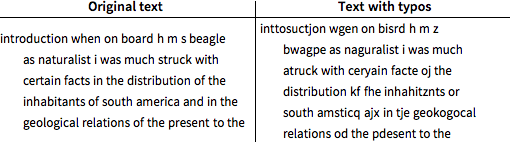 |
Tome los primeros 80.000 caracteres para ser una secuencia de prueba y el resto del texto como una secuencia de entrenamiento. La secuencia de prueba tiene el 16.5% de caracteres mal escritos, menos del 20% porque el carácter de espacio nunca fue mal escrito.
| In[7]:= |  X |
| Out[7]= |
Modele el flujo de caracteres escritos utilizando el proceso oculto de Markov. Los caracteres correctos son estados ocultos, mientras los caracteres escritos actuales son observaciones.
| In[8]:= |  X |
Estime el proceso oculto de Markov usando datos de entrenamiento.
| In[9]:= |  X |
| Out[9]= |
| In[10]:= |  X |
Utilice decodificación posterior para corregir errores tipográficos en la porción de prueba del texto mal escrito.
| In[11]:= |  X |
| Out[11]= |
El texto corregido aún presenta un 11% de errores tipográficos, 5.5% menos que el texto escrito original.
| Out[12]= | 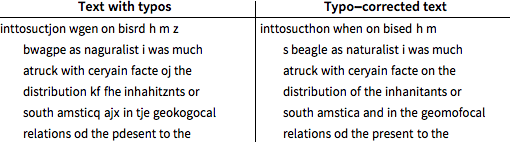 |
| In[13]:= |  X |
| Out[13]= |
Modele la evolución de los estados ocultos usando un proceso de Markov de segundo orden; es decir, asumir la probabilidad del carácter depende sólo de los dos caracteres anteriores. El proceso de Markov de segundo orden es modelado como un proceso de Markov de primer orden con espacio de estado ampliado de pares de caracteres consecutivos.
| In[14]:= |  X |
| In[15]:= | 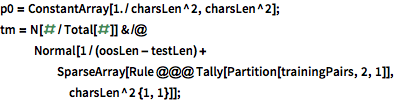 X |
La probabilidad del carácter escrito actual depende sólo del carácter real subyacente.
| In[16]:= | X |
Repita la decodificación posterior con el modelo oculto de Markov de orden superior.
| In[17]:= |  X |
| Out[17]= |
El porcentaje de errores tipográficos ha sido ahora reducido a menos de 6%.
| In[18]:= |  X |
| Out[18]= |
| Out[19]= | 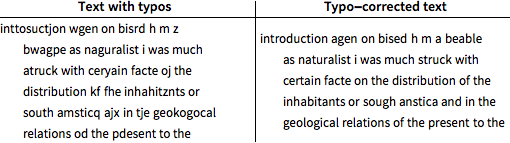 |




























