辞書なしでタイプミスの修正を実行する
タイプされた文字の列を観察として,正しい文字の列を隠れ状態としてモデリングするこの例では,正しい文字の進化に対する2つの異なるモデルを使ってタイプミスを修正する.最初のモデルは,指定された文字に続くものの頻度をエンコードするために,一次マルコフ過程を使う.2つ目のモデルは,指定された最後の2文字に続くものの頻度をエンコードするために二次マルコフ状態を使う.
ダーウィンの「The Origin of Species」を使い,文字以外のシンボルをすべてスペースに変換する.
| In[1]:= |  X |
| In[2]:= | X |
ランダムに文字を標準のQWERTYキーボードで隣り合う文字に置き換えて,20%の比率でタイプミスを導入する.スペース文字がタイプミスされることはない.
| In[4]:= |  X |
| In[5]:= |  X |
| Out[6]= | 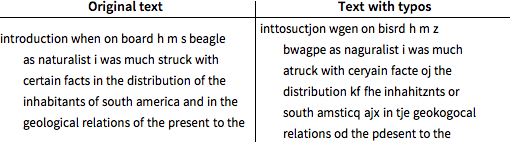 |
最初の80,000文字をテスト列として取り,残りのテキストは訓練列とする.テスト列には16.5%のタイプミスがある.これが20%に満たないのは,スペース文字がタイプミスされることはないからである.
| In[7]:= |  X |
| Out[7]= |
隠れマルコフ過程を使って,タイプされた文字のストリームをモデル化する.正しい文字は隠れ状態であり,実際にタイプされた文字は観察である.
| In[8]:= |  X |
訓練データを使って,隠れマルコフ過程を推測する.
| In[9]:= |  X |
| Out[9]= |
| In[10]:= |  X |
事後デコーディングを使って,タイプミスのあるテキストのテスト部分のスペルミスを修正する.
| In[11]:= |  X |
| Out[11]= |
修正されたテキストにはまだ11%のタイプミスがあるが,はじめにタイプされたテキストよりも5.5%少ない.
| Out[12]= | 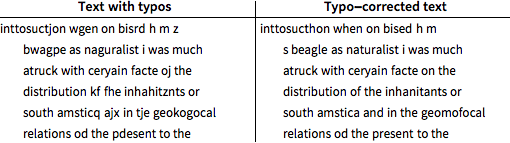 |
| In[13]:= |  X |
| Out[13]= |
二次マルコフ過程を使って,隠れ状態の進化をモデル化する.つまり,文字の確率は2つの先行する文字だけに依存すると想定するのである.二次マルコフ過程は連続する文字のペアの拡大状態空間を持つ一次マルコフ過程としてモデル化される.
| In[14]:= |  X |
| In[15]:= | 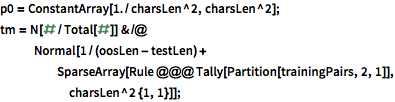 X |
実際にタイプされた文字の確率は,潜在する実際の文字だけに依存する.
| In[16]:= | X |
高次の隠れマルコフモデルで事後デコーディングを繰り返す.
| In[17]:= |  X |
| Out[17]= |
タイプミスの割合は6%未満にまで減少した.
| In[18]:= |  X |
| Out[18]= |
| Out[19]= | 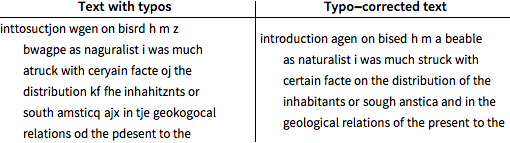 |




























